题目内容
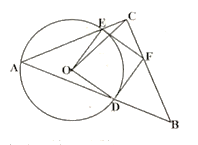
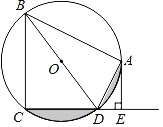
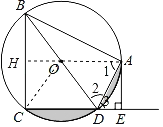
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,AD平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)如果AB=6,AE=3,求:阴影部分面积.
【答案】(1)见解析 (2)![]()
【解析】
(1)连接OA,利用已知首先得出OA∥DE,进而证明OA⊥AE就能得到AE是⊙O的切线;
(2)通过证明△BAD∽△AED,再利用对应边成比例关系从而求出⊙O半径的长,解直角三角形即可得到结论.
(1)证明:连接OA,
∵OA=OD,
∴∠1=∠2.
∵DA平分∠BDE,
∴∠2=∠3.
∴∠1=∠3.
∴OA∥DE.
∴∠OAE+∠AED=180°,
∵AE⊥CD,
∴![]()
∴∠OAE=90°,
即OA⊥AE.
又∵点A在⊙O上,
∴AE是⊙O的切线;
(2)解:∵BD是⊙O的直径,
∴∠BAD=90°.
∵∠AED=90°,
∴∠BAD=∠AED,
又∵∠2=∠3,
∴![]() .
.
∴![]()
∵BA=6,AE=3,
∴BD=2AD,
∴∠ABD=30°,
![]()
由![]()
∴BD=![]() ,
,
延长AO交BC于H,
则四边形AHCE是矩形,
∴∠AHC=90°,CH=AE=3,
∴BC=2CH=6,
∴cos∠CBD=![]()
∴∠CBD=30°,
∴∠COD=∠AOD=60°,![]()
由阴影部分面积=![]()
∴阴影部分面积=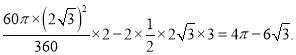

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目