题目内容
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

【答案】(1)①四边形CEGF是正方形;②![]() ;(2)线段AG与BE之间的数量关系为AG=
;(2)线段AG与BE之间的数量关系为AG=![]() BE;(3)3
BE;(3)3![]()
【解析】(1)①由![]() 、
、![]() 结合
结合![]() 可得四边形CEGF是矩形,再由
可得四边形CEGF是矩形,再由![]() 即可得证;
即可得证;
②由正方形性质知![]() 、
、![]() ,据此可得
,据此可得![]() 、
、![]() ,利用平行线分线段成比例定理可得;
,利用平行线分线段成比例定理可得;
(2)连接CG,只需证![]() ∽
∽![]() 即可得;
即可得;
(3)证![]() ∽
∽![]() 得
得![]() ,设
,设![]() ,知
,知![]() ,由
,由![]() 得
得![]() 、
、![]() 、
、![]() ,由
,由![]() 可得a的值.
可得a的值.
(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴![]() ,GE∥AB,
,GE∥AB,
∴![]() ,
,
故答案为:![]() ;
;
(2)连接CG,
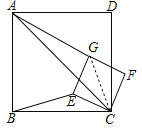
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,
![]() =cos45°=
=cos45°=![]() 、
、![]() =cos45°=
=cos45°=![]() ,
,
∴![]() =
=![]() ,
,
∴△ACG∽△BCE,
∴![]() ,
,
∴线段AG与BE之间的数量关系为AG=![]() BE;
BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴![]() ,
,
设BC=CD=AD=a,则AC=![]() a,
a,
则由![]() 得
得![]() ,
,
∴AH=![]() a,
a,
则DH=AD﹣AH=![]() a,CH=
a,CH=![]() =
=![]() a,
a,
∴由![]() 得
得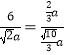 ,
,
解得:a=3![]() ,即BC=3
,即BC=3![]() ,
,
故答案为:3![]() .
.

【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
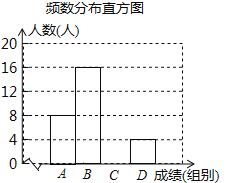
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .