题目内容
【题目】抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1,0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是( )
A.方程ax2+bx+c=2的一个根是x=﹣2
B.若x1=2,则抛物线与x轴的另一个交点为(﹣4,0)
C.若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2
D.若![]() ≤x≤0时,2≤y≤3,则a=
≤x≤0时,2≤y≤3,则a=![]()
【答案】D
【解析】
根据已知条件可将二次函数y=ax2+bx+c变形为y =a(x+1)2﹣a+2,把x=-2代入,可对A进行判断;利用对称性可对B进行判断;依据一元二次方程根的差别式可对C进行判断;根据抛物线的图象与性质可对D进行判断.
解:由已知可得,c=2,b=2a,
∴y=ax2+2ax+2=a(x2+2x)+2=a(x+1)2﹣a+2,
A.当x=﹣2时,y=2,
∴方程ax2+bx+c=2的一个根是x=﹣2;故A正确,不符合题意;
B.若x1=2,函数的对称轴为直线x=﹣1,则抛物线与x轴的另一个交点为(﹣4,0),正确,不符合题意;
C.ax2+2ax+2=4时,△=4a2+8a=0,
∴a=0或a=﹣2,
∴a=﹣2,正确,不符合题意;
D.若﹣![]() ≤x≤0时2≤y≤3;
≤x≤0时2≤y≤3;
在﹣![]() ≤x≤0时,当x=﹣1时,y有最大值2﹣a,当x=0时,有最最小值2;
≤x≤0时,当x=﹣1时,y有最大值2﹣a,当x=0时,有最最小值2;
∴3=2﹣a,
∴a=﹣1,
故D.错误,符合题意;
故选:D.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
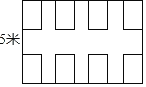
英才计划期末调研系列答案【题目】如图所示的是一个宽5米的餐厅,只能放8张餐桌.现计划扩建增加座位,只能对原宽度进行加长,设加长后的长度为m米.若餐厅的餐桌数为y,经计算,得到如下数据:(注:m和y都为正整数)
m(米) | 5 | 8 | 11 | 14 | …… |
餐桌数y(张) | 8 | 12 | 16 | …… |
(1)根据表中数据的规律,完成以上表格;
(2)求出y关于m的函数解析式;
(3)若这家餐厅至少要有80张餐桌,求m的最小值.