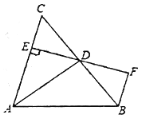
题目内容
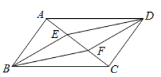
【题目】如图.![]() 平分
平分![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() 恰好平分
恰好平分![]() .
.
求证:(1)点![]() 为
为![]() 的中点;
的中点;
(2)![]() .
.
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)过点D作DH⊥AB于H,由角平分线的性质可得DE=DH,DF=DH,可得结论;
(2)由“AAS"可证△DCE≌△DBF,可证CD=BD,由等腰三角形的性质可证AD⊥BC;
(1)如图,过点D作DH⊥AB于H,
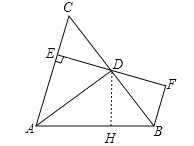
∵AD平分∠BAC,DE⊥AC,DH⊥AB,
∴DE=DH,
∵BF∥AC,DE⊥AC,
∴BF⊥DF,
∵BC平分∠ABF,DH⊥AB,DF⊥BF,
∴DF=DH,
∴DE=DF,
∴点D为EF的中点;
(2)∵BF∥AC,
∴∠C=∠DBF,
∵∠C=∠DBF,∠CDE=∠BDF,DE=DF,
∴△DCE≌△DBF,
∴CD=BD,
∵BC平分∠ABF,
∴∠ABD=∠DBF,
∴∠C=∠ABD,
∴AC=AB,且CD=BD,
∴AD⊥BC;

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目