题目内容
【题目】在平面直角坐标系xOy中，点M的坐标为（x1，y1），点N的坐标为（x2，y2），且x1≠x2，y1≠y2，以MN为边构造菱形，若该菱形的两条对角线分别平行于x轴，y轴，则称该菱形为边的“坐标菱形”．
（1）已知点A（1，0），B（0，
），则以AB为边的“坐标菱形”的最小内角为______；
（2）若点C（2，1），点D在直线y=5上，以CD为边的坐标菱形”为正方形，求育直线CD表达式；
（3）⊙O的半径为
，点P的坐标为（3，m），若在⊙O上存在一点Q，使得以QP为边的“坐标菱形”为正方形，求m的取值范围．
【答案】（1）60°；（2）y=x-1或y=-x+3；（3）m的取值范围是1≤m≤5或-5≤m≤-1．
【解析】
（1）根据定义建立以AB为边的“坐标菱形”，由勾股定理求边长AB=4，可得30度角，从而得最小内角为60°；
（2）先确定直线CD与直线y=5的夹角是45°，得D（6，5）或（-2，5），易得直线CD的表达式为：y=x-1或y=-x+3；
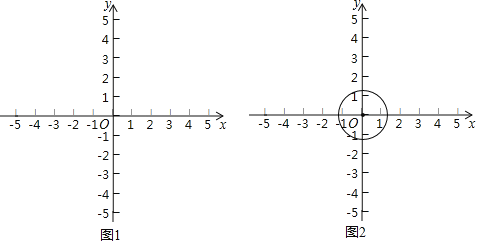
（3）分两种情况：①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3，根据等腰直角三角形的性质分别求P'B=BD=1，PB=5，写出对应P的坐标；
②先作直线y=-x，再作圆的两条切线，且平行于直线y=-x，如图4，同理可得结论．
解：（1）如图1中，
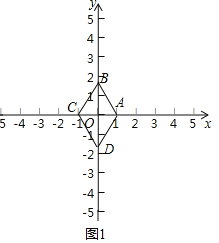
点A（1，0），B（0，
），
∴OA=1，OB=
，
在Rt△AOB中，由勾股定理得：AB=
=2，
∵sin∠ABO=
=
，
∴∠ABO=30°，
∵四边形ABCD是菱形，
∴∠ABC=2∠ABO=60°，
∵AB∥CD，
∴∠DCB=180°-60°=120°，
∴以AB为边的“坐标菱形”的最小内角为60°，
故答案为：60°；
（2）如图2中，
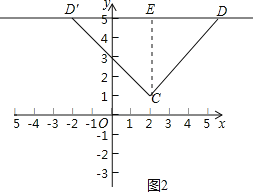
∵以CD为边的“坐标菱形”为正方形，
∴直线CD与直线y=5的夹角是45°．
过点C作CE⊥DE于E．
∴D（6，5）或（-2，5）．
∴直线CD的表达式为：y=x-1或y=-x+3；
（3）分两种情况：
①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3，
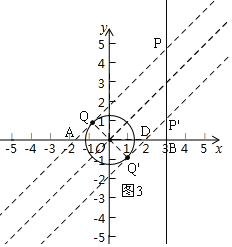
∵⊙O的半径为
，且△OQ'D是等腰直角三角形，
∴OD=OQ'=2，
∴P'D=3-2=1，
∵△P'DB是等腰直角三角形，
∴P'B=BD=1，
∴P'（0，1），
同理可得：OA=2，
∴AB=3+2=5，
∵△ABP是等腰直角三角形，
∴PB=5，
∴P（0，5），
∴当1≤m≤5时，以QP为边的“坐标菱形”为正方形；
②先作直线y=-x，再作圆的两条切线，且平行于直线y=-x，如图4，
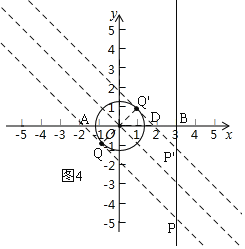
∵⊙O的半径为，且△OQ'D是等腰直角三角形，
∴OD=OQ'=2，
∴BD=3-2=1，
∵△P'DB是等腰直角三角形，
∴P'B=BD=1，
∴P'（0，-1），
同理可得：OA=2，
∴AB=3+2=5，
∵△ABP是等腰直角三角形，
∴PB=5，
∴P（0，-5），
∴当-5≤m≤-1时，以QP为边的“坐标菱形”为正方形；
综上所述，m的取值范围是1≤m≤5或-5≤m≤-1．
