Question

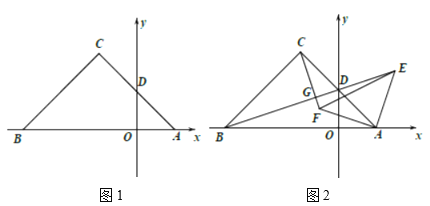
【题目】已知二次函数y＝ax2﹣（2a+1）x+c（a＞0）的图象经过坐标原点O，一次函数y＝﹣x+4与x轴、y轴分别交于点A、B．

（1）c＝　 　，点A的坐标为　 　；

（2）若二次函数y＝ax2﹣（2a+1）x+c的图象经过点A，求a的值；

（3）若二次函数y＝ax2﹣（2a+1）x+c的图象与△AOB只有一个公共点，直接写出a的取值范围．

Answer 1

【答案】（1）c=0，点 A 的坐标为（4，0）；（2）a=0.5；（3）a 的取值范围是．

【解析】

（1）根据题意和题目中的函数解析式可以求得c的值和点A的坐标；
（2）根据（1）中点A得坐标和二次函数y=ax2-（2a+1）x+c的图象经过点A，可以求得a的值；
（3）根据题意可以求得点B的坐标，然后根据二次函数与x轴的两个交点坐标为（0，0）和（，0），二次函数y=ax2-（2a+1）x+c的图象与△AOB只有一个公共点，可以求得a的取值范围．

（1）∵二次函数 y=ax2﹣（2a+1）x+c（a＞0）的图象经过坐标原点 O，

∴当 x=0 时，c=0，

将 y=0 代入 y=﹣x+4，得 x=4，即点 A 的坐标为（4，0）；

（2）∵二次函数 y=ax2﹣（2a+1）x+c 的图象经过点 A，点 A 的坐标为（4，0），

∴0=a×42﹣（2a+1）×4，

解得，a=0.5；

（3）将 x=0 代入 y=﹣x+4，得 y=4，即点 B 的坐标为（0，4），

∵点 A（4，0），点 O 的坐标为（0，0），二次函数 y=ax2﹣（2a+1）x 的图象与

△AOB 只有一个公共点，

，

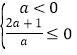解得，-≤a＜0．

即 a 的取值范围是，-≤a＜0．