Question

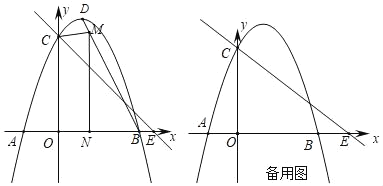
【题目】如图，过点C（1，2）分别作x轴、y轴的平行线，交直线y＝﹣x+8于A，B两点，若反比例函数y＝（x＞0）的图象与△ABC有公共点，则k的取值范围是_____．

Answer 1

【答案】

【解析】

根据题意可知当k最小时正好过点C，当直线y＝﹣x+8与反比例函数y＝（x＞0）只有一个交点时，k取得最大值，从而可以求得k的取值范围．

解：∵反比例函数y＝（x＞0）的图象与△ABC有公共点，过点C（1，2）分别作x轴、y轴的平行线，交直线y＝﹣x+8于A、B两点，

∴当y＝经过点C时，k=1×2

当反比例函数y＝（x＞0）的图象与△ABC有公共点，即y＝﹣x+8与y＝（x＞0）有交点，

∴方程﹣x+8＝有两个相等的根，

∴方程整理为：

∴△=64-4k≥0，解得，k≤16,

∴反比例函数y＝（x＞0）的图象与△ABC有公共点，则k的取值范围是2≤k≤16，

故答案为：2≤k≤16．