题目内容
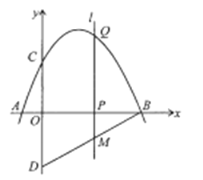
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴正半轴交于点
轴正半轴交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 与该抛物线交于
与该抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 位于点
位于点![]() 左侧),与抛物线对称轴交于点
左侧),与抛物线对称轴交于点![]() .
.
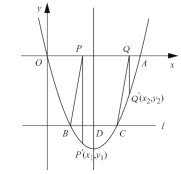
(1)求![]() 的值;
的值;
(2)设![]() 、
、![]() 是
是![]() 轴上的点(点
轴上的点(点![]() 位于点
位于点![]() 左侧),四边形
左侧),四边形![]() 为平行四边形.过点
为平行四边形.过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,与抛物线交于点
轴的垂线,与抛物线交于点![]() 、
、![]() .若
.若![]() ,求
,求![]() 、
、![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2) 或
或
【解析】
(1)根据直线![]() 与抛物线对称轴交于点
与抛物线对称轴交于点![]() 可得对称轴为直线
可得对称轴为直线![]() ,由此即可求得b 的值;
,由此即可求得b 的值;
(2)先求得点B、C的坐标,可得![]() ,再根据四边形
,再根据四边形![]() 为平行四边形可得
为平行四边形可得![]() ,即
,即![]() ,最后根据
,最后根据![]() ,
,![]() ,
,![]() 可得
可得![]() 或
或![]() ,由此分别与
,由此分别与![]() 联立方程组求解即可.
联立方程组求解即可.
解:(1)∵直线![]() 与抛物线
与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,
,
∴抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,
即![]() ,
,
∴![]() .
.
(2)由(1)得:抛物线的解析式为![]() ,
,
把![]() 代入抛物线的解析式
代入抛物线的解析式![]() ,
,
得![]() ,
,
解得![]() 或3,
或3,
∴![]() 、
、![]() 两点的坐标为
两点的坐标为![]() ,
,![]() ,
,
∴![]() ,
,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
由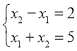 ,解得
,解得
由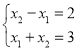 解得
解得
∴![]() 、
、![]() 的值为
的值为 或
或 .
.

练习册系列答案
相关题目