题目内容
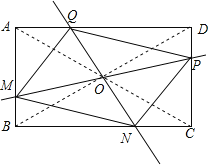
【题目】在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形,
其中正确的结论的个数为( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据矩形的判定和性质,菱形的判定,正方形的判定,平行四边形的判定定理即可得到结论.
解:①如图,∵四边形ABCD是矩形,连接AC,BD交于O,
过点O直线MP和QN,分别交AB,BC,CD,AD于M,N,P,Q,
则四边形MNPQ是平行四边形,
故存在无数个四边形MNPQ是平行四边形;故正确;
②如图,当PM=QN时,四边形MNPQ是矩形,故存在无数个四边形MNPQ是矩形;故正确;
③如图,当PM⊥QN时,存在无数个四边形MNPQ是菱形;故正确;
④当四边形MNPQ是正方形时,MQ=PQ,
则△AMQ≌△DQP,
∴AM=QD,AQ=PD,
∵PD=BM,
∴AB=AD,
∴四边形ABCD是正方形,
当四边形ABCD为正方形时,四边形MNPQ是正方形,故错误;
故选:C.

练习册系列答案
相关题目
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?