题目内容
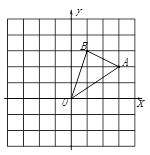
【题目】如图所示,已知抛物线y=ax2+bx+c过点A(﹣1,0),且经过直线y=x﹣3与坐标轴的两个交点B、C.
(1)求抛物线的表达式;
(2)若点M在第四象限内且在抛物线上,有OM⊥BC,垂足为D,求点M的坐标.

【答案】(1)y=x2﹣2x﹣3;(2)M点坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】【试题分析】
(1)先求出y=x﹣3与x轴的交点B的坐标为(3,0),与y轴的交点C的坐标为(0,﹣3),A点坐标为(﹣1,0),用交点式设二次函数解析式为y=a(x+1)(x﹣3),将C(0,﹣3)代入解析式得,﹣3=a×1×(﹣3),解得,a=1,则y=(x+1)(x﹣3),化为一般式得:y=x2﹣2x﹣3,
(2)由于OD过原点,则OD为正比例函数的图像,设OD的解析式为y=kx,
因为OM⊥BC,BC解析式为y=x-3,根据两条垂直的一次函数的k值互为相反数,得:
kOD=﹣1,则OD的解析式为y=﹣x,将y=x2﹣2x﹣3和y=﹣x组成方程组得![]() ,
,
解得,x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
把x1=![]() 代入y=﹣x得,y1=﹣
代入y=﹣x得,y1=﹣![]() ,
,
即M点坐标为(![]() ,﹣
,﹣![]() ).
).
【试题解析】
(1)∵y=x﹣3与x轴的交点B的坐标为(3,0),与y轴的交点C的坐标为(0,﹣3),A点坐标为(﹣1,0),
∴设二次函数解析式为y=a(x+1)(x﹣3),
将C(0,﹣3)代入解析式得,
﹣3=a×1×(﹣3),
解得,a=1,
则二次函数解析式为y=(x+1)(x﹣3),
即y=x2﹣2x﹣3,
(2)∵OD过原点,
∴设OD的解析式为y=kx,
∵OM⊥BC,BC解析式为y=x﹣3,
∴kOD=﹣1,
则OD的解析式为y=﹣x,
将y=x2﹣2x﹣3和y=﹣x组成方程组得![]() ,
,
整理得,x2﹣x﹣3=0,
解得,x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
把x1=![]() 代入y=﹣x得,
代入y=﹣x得,
y1=﹣![]() ,
,
∴M点坐标为(![]() ,﹣
,﹣![]() ).
).

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案