题目内容
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
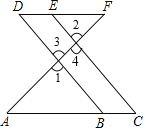
试说明:AC∥DF.
【答案】见解析
【解析】
试题根据已知条件∠1=∠2及对顶角相等求得同位角∠2=∠3,从而推知两直线DB∥EC,所以同位角∠C=∠ABD;然后由已知条件∠C=∠D推知内错角∠D=∠ABD,所以两直线AC∥DF.
解:∵∠1=∠2(已知) (1分)
∠1=∠3( 对顶角相等 ) (2分)
∴∠2=∠3(等量代换) (3分)
∴DB∥EC ( 同位角相等,两直线平行 ) (5分)
∴∠C=∠ABD ( 两直线平行,同位角相等 ) (7分)
又∵∠C=∠D(已知) (8分)
∴∠D=∠ABD( 等量代换 ) (10分)
∴AC∥DF( 内错角相等,两直线平行 ) (12分)

练习册系列答案
相关题目
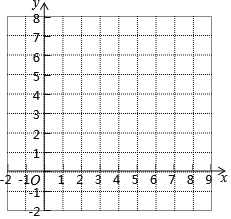
【题目】已知三角形A1B1C1是由三角形ABC经过平移得到的,其中A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如表所示:
三角形ABC | A(0,0) | B(﹣1,2) | C(2,5) |
三角形A1B1C1 | A1(a,2) | B1(4,b) | C1(7,7) |
(1)观察表中各对应点坐标的变化,填空a= ,b= ;
(2)在图中的平面直角坐标系中画出三角形ABC及三角形A1B1C1;
(3)P(m,n)为三角形ABC中任意一点,则平移后对应点P'的坐标为 .