题目内容
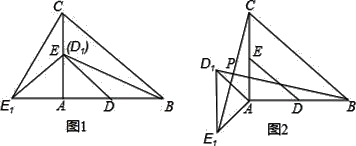
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x-m) 2+n的任意一条友好抛物线的解析式为y=a2 (x-h) 2+k,请写出a1与a2的关系式,并说明理由.

【答案】(1)点D坐标(4,4);(2)L4的解析式y=-2(x-4) 2+4,当2≤x≤4时,抛物线L3与L4中y同时随x增大而增大;(3)a1与a2的关系式为a1+a2=0或a1=-a2,理由见解析.
【解析】试题分析:(1)设x=0,求出y的值,即可得到C的坐标,把抛物线L3:y=2x2-8x+4配方即可得到抛物线的对称轴,由此可求出点C关于该抛物线对称轴对称的对称点D的坐标;
(2)由(1)可知点D的坐标为(4,4),再由条件以点D为顶点的L3的“友好”抛物线L4的解析式,可求出L4的解析式,进而可求出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得(a1+a2)(h-m)2=0.可得a1=-a2.
试题解析:(1)∵抛物线L3:y=2x28x+4,
∴y=2(x2)24,
∴顶点为(2,4),对称轴为x=2,
设x=0,则y=4,
∴C(0,4),
∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,4);
(2)∵以点D(4,4)为顶点的L3的友好抛物线L4还过点(2,4),
L4的解析式y=-2(x-4) 2+4,
由图象可知,当2≤x≤4时,抛物线L3与L4中y同时随x增大而增大;
(3)a1与a2的关系式为a1+a2=0或a1=-a2.
理由如下:
∵抛物线y=a1 (x-m) 2+n的一条“友好”抛物线的解析式为y=a2 (x-h) 2+k,
∴y=a2 (x-h) 2+k过点(m,n),且y=a1 (x-m) 2+n过点(h,k),
即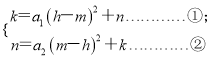
由①+②得(a1+a2) (h-m) 2=0.
又“友好”抛物线的顶点不重合,
∴h≠m,
∴a1+a2=0或a1=-a2.

 阅读快车系列答案
阅读快车系列答案