Question

【题目】已知二次函数（为常数）．

（1）求证：不论为何值，该二次函数的图像与轴总有公共点．

（2）求证：不论为何值，该二次函数的图像的顶点都在函数的图像上．

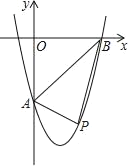
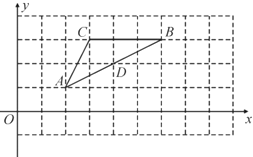
（3）已知点、，线段与函数的图像有公共点，则的取值范围是__________．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）计算判别式的值得到△≥0，从而根据判别式的意义得到结论；

（2）利用配方法得到二次函数y=x2-2mx+2m-1的顶点坐标为（m，-（m-1）2），然后根据二次函数图象上点的坐标特征进行判断；

（3）先计算出抛物线y=-（x-1）2与直线y=-1的交点的横坐标，然后结合图象得到a+2≥0且a≤2．

（1）令，则．

∵，，，

∴．

∵，

∴．

∴一元二次方程有实数根．

故不论取何值，函数与轴总有公共点．

（2）∵．

∴该函数的顶点坐标为．

把代入，得．

∴不论为何值，该二次函数的顶点坐标都在函数上．

（3）当y=-1时，y=-（x-1）2=-1，解得x1=0，x2=2，

当a+2≥0且a≤2时，线段AB与函数y=-（x-1）2的图象有公共点，

所以a的范围为-2≤a≤2．

故答案为．