题目内容
【题目】在四边形 ABCD 中,E 为 BC 边中点.
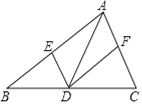
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD

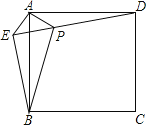
(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

【答案】(Ⅰ)(1)证明见解析;(2)证明见解析;(Ⅱ)(1)证明见解析;(2)证明见解析.
【解析】
(Ⅰ)(1)运用SAS证明△ABE≌AFE即可;
(2)由(1)得出∠AEB=∠AEF,BE=EF,再证明△DEF≌△DEC(SAS),得出DF=DC,即可得出结论;
(Ⅱ)(1)同(Ⅰ)(1)得△ABE≌△AFE(SAS),△DGE≌△DCE(SAS),由全等三角形的性质得出BE=FE,∠AEB=∠AEF,CE=GE,∠CED=∠GED,进而证明△EFG是等边三角形;
(2)由△EFG是等边三角形得出GF=EE=BE=![]() BC,即可得出结论.
BC,即可得出结论.
(Ⅰ)(1)∵AE平分∠BAD,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
 ,
,
∴△ABE≌△AFE(SAS),
(2)∵△ABE≌△AFE,
∴∠AEB=∠AEF,BE=EF,
∵E为BC的中点,
∴BE=CE,
∴FE=CE,
∵∠AED=∠AEF+∠DEF=90°,
∴∠AEB+∠DEC=90°,
∴∠DEF=∠DEC,
在△DEF和△DEC中,
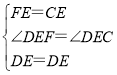 ,
,
∴△DEF≌△DEC(SAS),
∴DF=DC,
∵AD=AF+DF,
∴AD=AB+CD;
(Ⅱ)(1)∵E为BC的中点,
∴BE=CE=![]() BC,
BC,
同(Ⅰ)(1)得:△ABE≌△AFE(SAS),
△DEG≌△DEC(SAS),
∴BE=FE,∠AEB=∠AEF,CE=GE,∠CED=∠GED,
∵BE=CE,
∴FE=GE,
∵∠AED=120°,∠AEB+∠CED=180°-120°=60°,
∴∠AEF+∠GED=60°,
∴∠GEF=60°,
∴△EFG是等边三角形,
(2)∵△EFG是等边三角形,
∴GF=EF=BE=![]() BC,
BC,
∵AD=AF+FG+GD,
∴AD=AB+CD+![]() BC.
BC.