Question

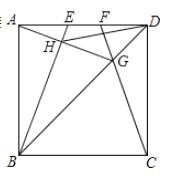
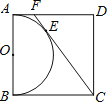
【题目】如图，以正方形ABCD的AB边为直径作半圆O，过点C作直线切半圆于点E，交AD边于点F，则＝（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

连接OE、OF、OC，利用切线长定理和切线的性质求出∠OCF＝∠FOE，证明△EOF∽△ECO，利用相似三角形的性质即可解答．

解：连接OE、OF、OC．

∵AD、CF、CB都与⊙O相切，

∴CE＝CB；OE⊥CF； FO平分∠AFC，CO平分∠BCF．

∵AF∥BC，

∴∠AFC+∠BCF＝180°，

∴∠OFC+∠OCF＝90°，

∵∠OFC+∠FOE＝90°，

∴∠OCF＝∠FOE，

∴△EOF∽△ECO，

∴，即OE2＝EFEC．

设正方形边长为a，则OE＝a，CE＝a．

∴EF＝a．

∴＝．

故选：C．