题目内容
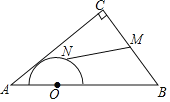
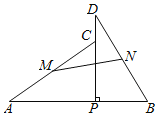
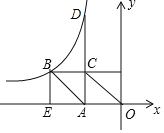
【题目】如图，已知反比例函数y＝
（x＜0）的图象经过OABC的顶点B，点A在x轴上，AC⊥x轴交反比例函数图象于点D，BE⊥x轴于点E，则BE：AD＝（ ）
A. 1：2B. 1：
C. 1：3D. 1：
【答案】A
【解析】
根据四边形ABCD是平行四边形，得到BC＝OA，根据已知条件得到BE∥AC，推出四边形ACBE是矩形，根据矩形的性质得到AE＝BC，得到OE＝2OA，设B（2x，
），D（x，
），于是得到结论．
解：∵四边形ABCD是平行四边形，
∴BC＝OA，
∵AC⊥x轴，BE⊥x轴，
∴BE∥AC，
∴四边形ACBE是矩形，
∴AE＝BC，
∴OE＝2OA，
设B（2x，），D（x，），
∴BE＝，AD＝，
∴BE：AD＝
＝
，
故选：A．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
【题目】商场里某产品每月销售量y（只）与销售单价x（元）满足一次函数关系，经调查部分数据如表：（已知每只进价为10元，每只利润=销售单价-进价）
销售单价x（元） | 21 | 23 | 25 | … |
月销售额y（只） | 29 | 27 | 25 | … |
（1）求出y与x之间的函数表达式；
（2）这产品每月的总利润为w元，求w关于x的函数表达式，并指出销售单价为多少元时利润最大，最大利润是多少元？
（3）由于该产品市场需求量较大，进价在原有基础上提高了a元（a＜10），但每月销售量与销售价仍满足上述一次函数关系，此时，随着销售量的增大，所得的最大利润比（2）中的最大利润减少了144元，求a的值．
