题目内容
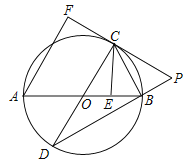
【题目】(2017广东省)如图,AB是⊙O的直径,AB=![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当![]() 时,求劣弧
时,求劣弧![]() 的长度(结果保留π)
的长度(结果保留π)
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题(1)、根据等角的余角相等证明即可;(2)、欲证明CF=CE,只要证明△ACF≌△ACE即可;(3)、作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=4a,PC=4a,PM=a,利用相似三角形的性质求出BM,求出tan∠BCM的值即可解决问题.
试题解析:(1)证明:∵OC=OB,∴∠OCB=∠OBC,∵PF是⊙O的切线,CE⊥AB,∴∠OCP=∠CEB=90°,∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,∴∠BCE=∠BCP,∴BC平分∠PCE.
(2)证明:连接AC.
∵AB是直径,∴∠ACB=90°,∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,∵∠BCP=∠BCE,∴∠ACF=∠ACE,∵∠F=∠AEC=90°,AC=AC,∴△ACF≌△ACE,∴CF=CE.
(3)解:作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=4a,PC=4a,PM=a,∵△BMC∽△PMB,∴![]() ,∴BM2=CMPM=3a2,∴BM=
,∴BM2=CMPM=3a2,∴BM=![]() a,∴tan∠BCM=
a,∴tan∠BCM=![]() ,∴∠BCM=30°,∴∠OCB=∠OBC=∠BOC=60°,∴
,∴∠BCM=30°,∴∠OCB=∠OBC=∠BOC=60°,∴![]() 的长=
的长=![]() =
=![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此九(2)班数学兴趣小组对本班同学天饮用饮品的情况进行了调查,发现大致可分为四种:A非碳酸饮料,B瓶装矿泉水,C碳酸饮料,D白开水.
根据统计结果绘制如下两个统计图,根据统计图提供的信息解答下列问题:
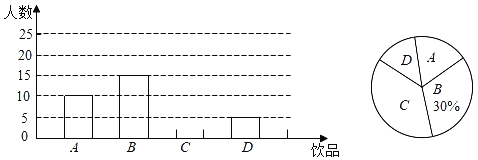
(1)九(2)班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名同学(其中有两位班长记为a,b,其余三位记为c,d,e)中随机抽取2名作良好习惯监督员,请用列表法或画树状图的方法,求出抽到的2名同学都不是班长的概率.