��Ŀ����
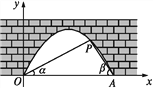
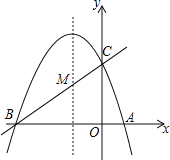
����Ŀ����ͼ����֪������y��ax2+bx+c(a��0)�ĶԳ���Ϊֱ��x����1���������߾���A(1��0)��C(0��3)���㣬��x�ύ�ڵ�B��
(1)��ֱ��y��mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
(2)�������ߵĶԳ���x����1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
(3)���PΪ�����ߵĶԳ���x����1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
���𰸡�(1)�����߽���ʽΪy����x2��2x+3��ֱ�ߵĽ���ʽΪy��x+3��(2)����M����A�ľ����뵽��C�ľ���֮����СʱM������Ϊ(��1��2)��(3)P������Ϊ(��1����2)��(��1��4)��(��1��![]() ) ��(��1��
) ��(��1��![]() )��
)��
��������
![]() �Ȱѵ�A��C������ֱ���������߽���ʽ�õ�a��b��c�Ĺ�ϵʽ���ٸ��������ߵĶԳ��᷽�̿ɵ�a��b�Ĺ�ϵ���������õ������飬�ⷽ���飬���a��b��c��ֵ���ɵõ������߽���ʽ����B��C������������ֱ��
�Ȱѵ�A��C������ֱ���������߽���ʽ�õ�a��b��c�Ĺ�ϵʽ���ٸ��������ߵĶԳ��᷽�̿ɵ�a��b�Ĺ�ϵ���������õ������飬�ⷽ���飬���a��b��c��ֵ���ɵõ������߽���ʽ����B��C������������ֱ��![]() ���ⷽ�������m��n��ֵ���ɵõ�ֱ�߽���ʽ��
���ⷽ�������m��n��ֵ���ɵõ�ֱ�߽���ʽ��
![]() ��ֱ��BC��Գ���
��ֱ��BC��Գ���![]() �Ľ���ΪM�����ʱ
�Ľ���ΪM�����ʱ![]() ��ֵ��С
��ֵ��С![]() ��
��![]() ����ֱ��
����ֱ��![]() ��y��ֵ�����������M���ꣻ
��y��ֵ�����������M���ꣻ
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() �����Կɵ�
�����Կɵ�![]() ��
��![]() ��
��![]() ���ٷ���������ֱ����������������tֵ���������P�����꣮
���ٷ���������ֱ����������������tֵ���������P�����꣮
�⣺(1)������ã�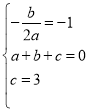 ��
��
��֮�ã� ��
��
�������߽���ʽΪy����x2��2x+3
���Գ���Ϊx����1���������߾���A(1��0)��
����B(��3��0)��C(0��3)�ֱ����ֱ��y��mx+n��
��![]() ��
��
��֮�ã�![]() ��
��
��ֱ��y��mx+n�Ľ���ʽΪy��x+3��
(2)��ֱ��BC��Գ���x����1�Ľ���ΪM�����ʱMA+MC��ֵ��С��
��x����1����ֱ��y��x+3�ã�y��2��
��M(��1��2)��
������M����A�ľ����뵽��C�ľ���֮����СʱM������Ϊ(��1��2)��
(3)��P(��1��t)��
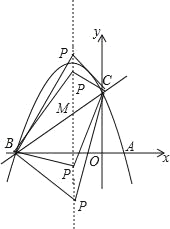
����B(��3��0)��C(0��3)��
��BC2��18��PB2��(��1+3)2+t2��4+t2��PC2��(��1)2+(t��3)2��t2��6t+10��
������BΪֱ�Ƕ��㣬��BC2+PB2��PC2����18+4+t2��t2��6t+10��֮�ã�t����2��
������CΪֱ�Ƕ��㣬��BC2+PC2��PB2����18+t2��6t+10��4+t2��֮�ã�t��4��
������PΪֱ�Ƕ��㣬��PB2+PC2��BC2����4+t2+t2��6t+10��18��֮�ã�t1��![]() ��t2��
��t2��![]() ��
��
��������P������Ϊ(��1����2)��(��1��4)��(��1��![]() ) ��(��1��
) ��(��1��![]() )��
)��