��Ŀ����
����Ŀ���̳���ij��Ʒÿ��������y��ֻ�������۵���x��Ԫ������һ�κ�����ϵ�������鲿���������������֪ÿֻ����Ϊ10Ԫ��ÿֻ����=���۵���-���ۣ�
���۵���x��Ԫ�� | 21 | 23 | 25 | �� |
�����۶�y��ֻ�� | 29 | 27 | 25 | �� |
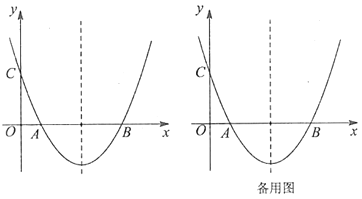
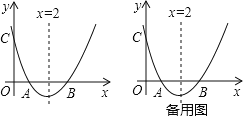
��1�����y��x֮��ĺ�������ʽ��
��2�����Ʒÿ�µ�������ΪwԪ����w����x�ĺ�������ʽ����ָ�����۵���Ϊ����Ԫʱ���������������Ƕ���Ԫ��
��3�����ڸò�Ʒ�г��������ϴ�����ԭ�л����������aԪ��a��10������ÿ�������������ۼ�����������һ�κ�����ϵ����ʱ���������������������õ��������ȣ�2���е�������������144Ԫ����a��ֵ��
���𰸡���1��y=-x+50����2�������۵��۶�Ϊ30Ԫʱ��ÿ�¿ɻ���������400Ԫ����3��8��
��������
![]() ����ϵ������������ʽ��
����ϵ������������ʽ��
![]() ������
������![]() ��������
��������![]() �����������ȱ�ʾ��w���ٸ��ݶ��κ�������ֵ��������䷽���ɣ�
�����������ȱ�ʾ��w���ٸ��ݶ��κ�������ֵ��������䷽���ɣ�
![]() ���εĶ��κ������⣬�ȱ�ʾ��w��������������з��̼������a��
���εĶ��κ������⣬�ȱ�ʾ��w��������������з��̼������a��
�⣺��1����y=kx+b��k��0����
�����������㣨21��29������25��25����
��![]()
���![]() ��
��
��y=-x+50��
��2��������ã�w=��x-10����-x+50��=-x2+60x-500=-��x-30��2+400��
��a=-1��0��
�൱x=30ʱ��w�����ֵ400��
�������۵��۶�Ϊ30Ԫʱ��ÿ�¿ɻ���������400Ԫ��
��3����������ɱ�ʾΪ-x2+60x-500-a��-x+50��=-x2+��60+a��x-500-50a��
���ʱ�������Ϊ![]() =400-144��
=400-144��
���a1=8��a2=72��
�ߵ�a=72ʱ������Ϊ������ȥ��
��a=8��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ������ʦ�������̵ľţ�1�����ţ�2�������༶��ѧ��������һ�μ�⣬���ĺ�����һ������ĵ÷���������˹���ͳ�ƣ������ĵ÷����±���������������ͼ��ʾ��ÿ������÷�����������ͳ��ͼ������������
�����ĵ÷ֱ�
�÷� | ��� |
|
|
|
|
|
|
|
|
��֪������һ����![]() ��ѧ���õ�������ȷ�𰸣������ȫ��ȷ���ţ�1����ѧ����������ƽ���÷�Ϊ
��ѧ���õ�������ȷ�𰸣������ȫ��ȷ���ţ�1����ѧ����������ƽ���÷�Ϊ![]() �֣������������⣺
�֣������������⣺
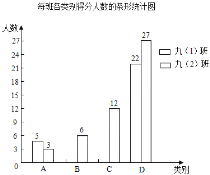
��1���ţ�2����ѧ���÷ֵ���λ���� ______��
��2���ţ�1����ѧ����������������������![]() ���
���![]() ����������Ƕ��٣�
����������Ƕ��٣�