题目内容
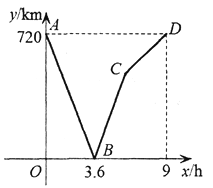
【题目】一辆快车与一辆慢车分别从甲、乙两地同时出发，沿同一路线相向 而行，抵达对方出发地时停止运动．设慢车行驶xh时，两车之间的路程为ykm．图中折线ABCD表示y与x的函数关系，根据图像，解决以下问题：
(1)慢车的速度为多少km／h，快车的速度为多少km／h；
(2)解释图中点C的实际意义，求出点C的坐标；
(3)当x取何值时，y＝500 ?
【答案】(1)80，120；(2)点C表示时间为6h快车到达乙地并停止运动，(6，480)；(3)x=1.1或6.25.
【解析】
(1)由图象可知甲乙两地相距720km，慢车走完全程需要9h，即可求出慢车的速度，根据两车3.6h相遇，便可求也快车的速度；
(2)利用图象得出点C表示时间为6h，快车到达乙地并停止运动，此时点C坐标为(6，480)；
(3)两车相遇之前和两车相遇之后都会出现y=500的情况，相遇之前500表示两车未走的路程，相遇之后500表示两车走过的路程，分别列方程解答即可.
解：(1)由图象可知甲乙两地相距720km，慢车走完全程需要9h，
慢车的速度为：720÷9=80(km/h)，
由图象可知两车出发后3.6h相遇，则两车速度和为：720÷3.6=200km/h，
快车的速度为：200-80=120(km/h)；
(2)点C的实际意义是：当时间为6h时，快车到达乙地并停止运动，
720÷120=6h，80×6=480km，
∴点C的坐标为(6，480)；
(3)由图象可知，两车相遇时间3.6h，y=500时，有以下两种情况：
①两车相遇之前：120x+80x=720-500,解得x=1.1;
②两车相遇之后：由点C意义可知，快车到达乙地时，两车相遇480km，
∴500-480=80(x-6)，解得x=6.25，
所以当x=1.1或6.25时，y=500.
故答案为：(1)80，120；(2)点C表示时间为6h快车到达乙地并停止运动，(6，480)；(3)x=1.1或6.25.
