ЬтФПФкШн
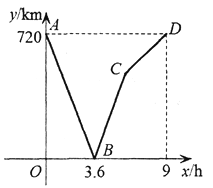
ЁОЬтФПЁПаЁУїКЭАжАжДгМвВНааШЅЙЋдАЃЌАжАжЯШГіЗЂвЛжБдШЫйЧАааЃЌаЁУїКѓГіЗЂдШЫйЧАааЃЌЧвЭОжаанЯЂвЛЖЮЪБМфКѓМЬајвддЫйЧАааЃЎМвЕНЙЋдАЕФОрРыЮЊ2000mЃЌШчЭМЪЧаЁУїКЭАжАжЫљзпЕФТЗГЬSЃЈmЃЉгыВНааЪБМфtЃЈminЃЉЕФКЏЪ§ЭМЯѓЃЎ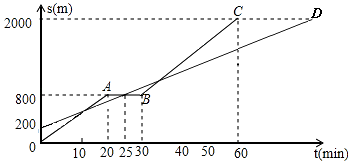
ЃЈ1ЃЉжБНгаДГіBCЖЮЭМЯѓЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЈВЛгУаДГіtЕФШЁжЕЗЖЮЇЃЉЃЎ
ЃЈ2ЃЉаЁУїГіЗЂЖрЩйЪБМфгыАжАжЕкШ§ДЮЯргіЃП
ЃЈ3ЃЉдкЫйЖШЖМВЛБфЕФЧщПіЯТЃЌаЁУїЯЃЭћБШАжАждч18ЗжжгЕНДяЙЋдАЃЌдђаЁУїдкВНааЙ§ГЬжаЭЃСєЕФЪБМфашМѕЩйЗжжгЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЩшжБЯпBCЫљЖдгІЕФКЏЪ§БэДяЪНЮЊs=kt+bЃЌ
НЋЃЈ30ЃЌ800ЃЉЃЌЃЈ60ЃЌ2000ЃЉДњШыЕУ
![]() ЃЌ
ЃЌ
НтЕУ ![]() ЃЌ
ЃЌ
ЁржБЯпBCЫљЖдгІЕФКЏЪ§БэДяЪНЮЊs=40tЉ400
ЃЈ2ЃЉНтЃКЩшаЁУїЕФАжАжЫљзпТЗГЬsгыЪБМфtЕФКЏЪ§ЙиЯЕЪНЪЧs=mt+nЃЌ
дђ ![]() ЃЌНтЕУ
ЃЌНтЕУ ![]() ЃЌ
ЃЌ
МДаЁУїЕФАжАжЫљзпТЗГЬsгыЪБМфtЕФКЏЪ§ЙиЯЕЪНЪЧs=24t+200ЃЌ
НтЗНГЬзщ ![]() ЃЌЕУ
ЃЌЕУ ![]() ЃЌ
ЃЌ
МДаЁУїГіЗЂ37.5minЪБгыАжАжЕкШ§ДЮЯргі
ЃЈ3ЃЉ3
ЁОНтЮіЁПЃЈ3ЃЉЕБs=2000ЪБЃЌ2000=24t+200ЃЌЕУt=75ЃЌ
Ёп75Љ60=15ЃЌ
ЁраЁУїЯЃЭћБШАжАждч18minЕНДяЙЋдАЃЌдђаЁУїдкВНааЙ§ГЬжаЭЃСєЕФЪБМфашвЊМѕЩй3minЃЎ
ЫљвдД№АИЪЧ3ЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтШЗЖЈвЛДЮКЏЪ§ЕФБэДяЪНЕФЯрЙижЊЪЖЃЌеЦЮеШЗЖЈвЛИівЛДЮКЏЪ§ЃЌашвЊШЗЖЈвЛДЮКЏЪ§ЖЈвхЪНy=kx+bЃЈkВЛЕШгк0ЃЉжаЕФГЃЪ§kКЭbЃЎНтетРрЮЪЬтЕФвЛАуЗНЗЈЪЧД§ЖЈЯЕЪ§ЗЈЃЎ

 ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ
ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИЁОЬтФПЁПЮЪЬтБГОАЃК
аЁКьЭЌбЇдкбЇЯАЙ§ГЬжагіЕНетбљвЛЕРМЦЫуЬтЁАМЦЫу4ЁС3.142Љ4ЁС3.14ЁС3.28+3.282ЁБЃЌЫћОѕЕУЬЋТщЗГЃЌЙРМЦгІИУгаПЩвдМђЛЏМЦЫуЕФЗНЗЈЃЌОЭШЅЧыНЬДоРЯЪІЃЎДоРЯЪІЫЕЃКФуЭъГЩЯТУцЕФЮЪЬтКѓОЭПЩФмжЊЕРИУШчКЮМђЛЏМЦЫуРВЃЁ
ЛёШЁаТжЊЃК
ЧыФуКЭаЁКьвЛЦ№ЭъГЩДоРЯЪІЬсЙЉЕФЮЪЬтЃК
ЃЈ1ЃЉЬюаДЯТБэЃК
x=Љ1ЃЌy=1 | x=1ЃЌy=0 | x=3ЃЌy=2 | x=1ЃЌy=1 | x=5ЃЌy=3 | |
A=2xЉy | Љ3 | 2 | 4 | 1 | 7 |
B=4x2Љ4xy+y2 | 9 | 4 | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЃЈ2ЃЉЙлВьБэИёЃЌФуЗЂЯжAгыBгаЪВУДЙиЯЕЃП
НтОіЮЪЬтЃК
ЃЈ3ЃЉЧыНсКЯЩЯЪіЕФгаЙиаХЯЂЃЌМЦЫу4ЁС3.142Љ4ЁС3.14ЁС3.28+3.282ЃЎ