题目内容
【题目】【发现】:如图1,在正三角形ABC中,在AB,AC边上分别取点M,N,BM=AN,连接BN,CM,相交于点O,求∠α
易得:△ABN≌△BCN,则∠1=∠2
∵∠α是△BOC的外角,∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°
【推广】:在正n边形中,对相邻的两边实施同样的操作…
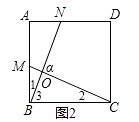
(1)如图2,在正四边形ABCD中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(2)如图3,在正五边形ABCDE中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(3)判断:∠α可以等于160°吗?如果可以,求出对应的边数n,若不可以,说明理由.
【答案】
(1)90
(2)108
(3)解:∠α可以等于160°,
理由:由于上述操作发现的结论可知,正n边形中的∠α=正n边形的内角的度数,
假设存在正n边形使得∠α=160°,则(n﹣2)180°=160°n,
解得:n=18,
∴存在正n边形使得∠α=160°,
此时,该正n边形为正十八边形.
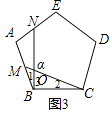
【解析】解:(1)∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBM=90°,
在△ABN与△BCM中, 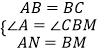 ,
,
∴△ABN≌△BCM,
∴∠1=∠2,
∵∠α是△BOC的外角,
∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=90°;
所以答案是:90;(2)∵四边形ABCD是正五边形,
∴AB=BC,∠A=∠CBM=108°,
在△ABN与△BCM中, 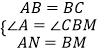 ,
,
∴△ABN≌△BCM,
∴∠1=∠2,
∵∠α是△BOC的外角,
∴∠α=∠2+∠3,
∴∠α=∠1+∠3=∠ABC=108°;
所以答案是:108;

练习册系列答案
相关题目