题目内容
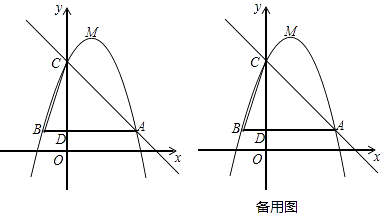
【题目】如图①，将两个边长为1的小正方形分别沿对角线剪开，拼成正方形ABCD．
（1）正方形ABCD的面积为 ，边长为 ，对角线BD= ；
（2）求证：
；
（3）如图②，将正方形ABCD放在数轴上，使点B与原点O重合，边AB落在x轴的负半轴上，则点A所表示的数为 ，若点E所表示的数为整数，则点E所表示的数为 ．
【答案】（1）2，
，2；（2）证明见解析；（3）
，
．
【解析】
（1）由图形拼接不改变面积，边长是面积的算术平方根，以及勾股定理可得答案，
（2）利用变形前后面积不变证明
，
（3）由
的长度结合
的位置直接得到答案，再利用数轴上数的大小分布得到
表示的数．
解：（1）由图形拼接不改变面积可得：
正方形ABCD＝
由边长是面积的算术平方根可得：正方形ABCD的边长为
由拼接可得
大正方形的面积
（负根舍去）
故答案为：2，，2；
（2）小正方形的面积
由拼接可得：
大正方形的面积
，
（3）由（1）知：
在数轴负半轴上，
点表示
在
之间且表示整数，
表示
故答案为：，．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
