题目内容
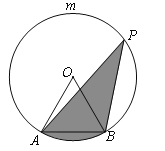
【题目】如图,已知二次函数y=![]() +bx+c的图象交x轴于点A,B,交y轴于点C(0,﹣2),一次函数y=
+bx+c的图象交x轴于点A,B,交y轴于点C(0,﹣2),一次函数y=![]() x+n的图象经过A,C两点,点P为直线AC下方二次函数图象上的一个动点,直线BP交线段AC于点E,PF⊥AC于点F.
x+n的图象经过A,C两点,点P为直线AC下方二次函数图象上的一个动点,直线BP交线段AC于点E,PF⊥AC于点F.
(1)求二次函数的解析式;
(2)求![]() 的最大值及此时点P的坐标;
的最大值及此时点P的坐标;
(3)连接CP,是否存在点P,使得Rt△CPF中的一个锐角恰好等于2∠BAC?若存在,请直接写出点P的坐标;否则,说明理由.

【答案】(1)y=![]() ;(2)m=2时,
;(2)m=2时,![]() 有最大值为
有最大值为![]() ,此时P点坐标为(2,﹣3);(3)P点坐标是(2,﹣3)或
,此时P点坐标为(2,﹣3);(3)P点坐标是(2,﹣3)或![]()
【解析】
(1)求出A点坐标,根据待定系数法,可得函数解析式;
(2)过点B作BM∥y轴交AC于点M,过点P作PN∥y轴交AC于点N,可得PN∥BM,则△BME∽△PNE,则![]() ,可求出BM=
,可求出BM=![]() ,设P(
,设P(![]() ),可表示PN长,则可得关于m的二次函数,根据二次函数的性质,可得答案;
),可表示PN长,则可得关于m的二次函数,根据二次函数的性质,可得答案;
(3)根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点D,求得D(![]() ,0),得到DA=DC=DB=
,0),得到DA=DC=DB=![]() ,过P作x轴的平行线交y轴于R,交AC于G,情况一:如图,∠PCF=2∠BAC=∠DGC+∠CDG,情况二,∠FPC=2∠BAC,解直角三角形即可得到结论.
,过P作x轴的平行线交y轴于R,交AC于G,情况一:如图,∠PCF=2∠BAC=∠DGC+∠CDG,情况二,∠FPC=2∠BAC,解直角三角形即可得到结论.
解:(1)由C(0,﹣2),可知一次函数解析式为y=![]() ,
,
当y=0时,x=4,即A(4,0),
将A,C点坐标代入函数解析式,得
![]() ,
,
解得: ,
,
抛物线的解析是为y=![]() ;
;
(2)如图1,过点B作BM∥y轴交AC于点M,过点P作PN∥y轴交AC于点N,

∴PN∥BM,
∴△BME∽△PNE,
∴![]() ,
,
∵B(﹣1,0),
∴x=﹣1时,y=﹣![]() ,
,
∴M(﹣1,﹣![]() ,
,
∴BM=![]() ,
,
设P(![]() ),则N(
),则N(![]() ),
),
∴![]() ,
,
![]() ,
,
∴当m=2时,![]() 有最大值为
有最大值为![]() ,此时P点坐标为(2,﹣3);
,此时P点坐标为(2,﹣3);
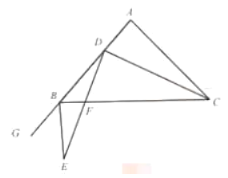
(3)如图2,
∵A(4,0),B(﹣1,0),C(0,﹣2),
∴AC=![]() ,BC=
,BC=![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC是以∠ACB为直角的直角三角形,取AB的中点D,
∴D(![]() ,0),
,0),
∴DA=DC=DB=![]() ,
,
∴∠CDO=2∠BAC,
∴tan∠CDO=tan(2∠BAC)=![]() ,
,
过P作x轴的平行线交y轴于R,交AC的延长线于G,
情况一:如图2,
∵∠PCF=2∠BAC=∠PGC+∠CPG,
∴∠CPG=∠BAC,
∴tan∠CPG=tan∠BAC=![]() ,
,
即![]() ,
,
设P(a,![]() ),
),
∴PR=a,RC=﹣![]() ,
,
∴ ,
,
∴a1=0(舍去),a2=2,
∴xP=2,y=![]() ,P(2,﹣3),
,P(2,﹣3),
情况二,∴∠FPC=2∠BAC,
∴tan∠FPC=![]() ,
,
设FC=4k,
∴PF=3k,PC=5k,
∴FG=6k,
∴CG=2k,PG=![]() k,
k,
∴![]() ,
,
∴![]() ,
,
∴ ,
,
∴a1=0(舍去),![]() ,
,
x=![]() 时,y=﹣
时,y=﹣![]() ,
,
即P![]() .
.
综上所述:P点坐标是(2,﹣3)或![]()

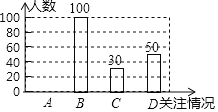
【题目】2019年2月18日,“时代楷模”、伏牛山里的好教师﹣﹣张玉滚当选“感动中国”2018年度人物,在中原大地引起强烈反响.为了解学生对张玉滚事迹的知晓情况,某数学课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A,B,C,D四类,将调查的数据整理后绘制成如下统计表及条形统计图(均不完整):
关注情况 | 频数 | 频率 |
A.非常了解 | m | 0.1 |
B.比较了解 | 100 | 0.5 |
C.基本了解 | 30 | n |
D.不太了解 | 50 | 0.25 |
根据以上信息解答下列问题:
(1)在这次抽样调查中,一共抽查了 名学生;
(2)统计表中,m= ,n= ;
(3)请把条形统计图补充完整;
(4)该校共有学生1500名,请你估算该校学生中对张玉滚事迹“非常了解“和“比较了解”的学生共有多少名.