Question

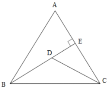
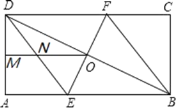
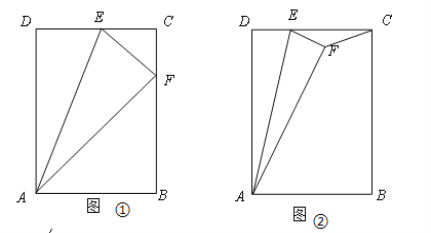
【题目】在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，将△ABC绕点A顺时针旋转60°，得到△AED，点B、C的对应点分别是E、D．F为AC的中点，连接BF、DF、BE，DF与EA相交于点G，BE与AC相交于点H．

（1）如图1，求证：四边形BFDE为平行四边形；

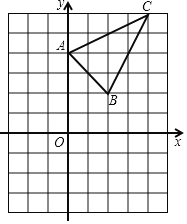
（2）如图2，连接CE，在不添加任何辅助线与字母的情况下，请直接写出所有与△AEC全等的三角形．

Answer 1

【答案】（1）见解析；（2）△ADE，△ABC，△ADF与△ACE全等，理由见解析

【解析】

（1）由直角三角形的性质可得BF＝BC，由旋转的性质可得∠ACB＝∠DAF＝60°，CA＝DA，AF＝CB，由“SAS”可证△AFD≌△CBA，可得DF＝AB＝BE，且BF＝DE，即可得四边形BFDE是平行四边形；

（2）由“SAS”可证△BAC≌△EAC，△ACE≌△ADE，可求解．

证明：（1）∵点F是边AC中点，∠ABC＝90°，

∴BF＝AC，

又∵∠BAC＝30°，

∴BC＝AC，∠ACB＝60°，

∴BF＝BC，

∵将△ABC绕点A顺时针旋转60°，得到△AED，

∴∠BAE＝∠DAC＝60°，CA＝DA，DE＝BC，

∴DE＝BF，△BCF和△BAE为等边三角形，

∴BE＝AB＝AE，

∴AF=BC，∠CAD＝∠C＝60°，AC＝AD，

∴△AFD≌△CBA（SAS），

∴DF＝AB，

∴DF＝BE，且BF＝DE，

∴四边形BFDE是平行四边形；

（2）△ADE，△ABC，△ADF与△ACE全等；

理由如下：由（1）可得：

∵∠BAE＝60°，∠BAC＝30°，

∴∠BAC＝∠CAE＝30°，且AC＝AC，AB＝AE，

∴△BAC≌△EAC（SAS），

∵∠CAE＝∠DAE＝30°，AC＝AD，AE＝AE，

∴△ACE≌△ADE（SAS），

∵△AFD≌△CBA（已证），

∴△EAC≌△FDA．

故：△ADE，△ABC，△ADF与△ACE全等