题目内容
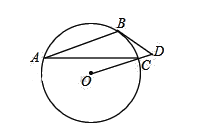
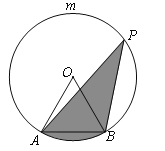
【题目】如图,AB是⊙O的弦,AB=4,点P在![]() 上运动(点P不与点A、B重合),且∠APB=30°,设图中阴影部分的面积为y.
上运动(点P不与点A、B重合),且∠APB=30°,设图中阴影部分的面积为y.
(1)⊙O的半径为 ;
(2)若点P到直线AB的距离为x,求y关于x的函数表达式,并直接写出自变量x的取值范围.
【答案】(1)4;(2)y=2x+![]() π-4
π-4![]() (0<x≤2
(0<x≤2![]() +4)
+4)
【解析】
(1)根据圆周角定理得到△AOB是等边三角形,求出⊙O的半径;
(2)过点O作OH⊥AB,垂足为H,先求出AH=BH=![]() AB=2,再利用勾股定理得出OH的值,进而求解.
AB=2,再利用勾股定理得出OH的值,进而求解.
(1)解:(1)∵∠APB=30°,
∴∠AOB=60°,又OA=OB,
∴△AOB是等边三角形,
∴⊙O的半径是4;
(2)解:过点O作OH⊥AB,垂足为H

则∠OHA=∠OHB=90°
∵∠APB=30°
∴∠AOB=2∠APB=60°
∵OA=OB,OH⊥AB
∴AH=BH=![]() AB=2
AB=2
在Rt△AHO中,∠AHO=90°,AO=4,AH=2
∴OH=![]() =2
=2![]()
∴y=![]() ×16 π-
×16 π-![]() ×4×2
×4×2![]() +
+![]() ×4×x
×4×x
=2x+![]() π-4
π-4![]() (0<x≤2
(0<x≤2![]() +4).
+4).

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
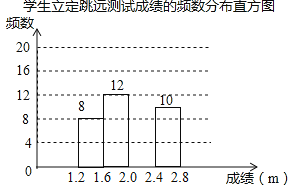
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?