题目内容
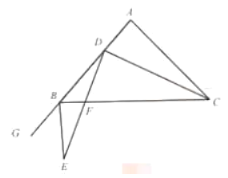
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点(点
上的动点(点![]() 不与点
不与点![]() 重合),点
重合),点![]() 在边
在边![]() 的延长线上,
的延长线上,![]() ,
,![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)点![]() 在边
在边![]() 上运动的过程中,
上运动的过程中,![]() 的值是否会发生变化?如果不变化,请求
的值是否会发生变化?如果不变化,请求![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)作AH⊥BC于H,BM⊥AC于M.解直角三角形求出BM,AM即可解决问题.
(2)设AH交CD于K.首先证明AK=CK,设AK=CK=x,在Rt△CHK中,理由勾股定理求出x,再证明△ADK∽△CDA,理由相似三角形的性质构建方程组即可解决问题.
(3)结论:AD:BE=5:6值不变.证明△ACD∽△BCE,可得![]() .
.
(1)作AH⊥BC于H,BM⊥AC于M.
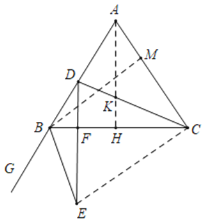
∵AB=AC,AH⊥BC,
∴BH=CH=3,
∴![]() ,
,
∵![]() ,
,
∴BM=![]() ,
,
∴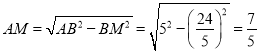 ,
,
∴![]() .
.
(2)设AH交CD于K.
∵∠BAC=2∠ACD,∠BAH=∠CAH,
∴∠CAK=∠ACK,
∴CK=AK,设CK=AK=x,
在Rt△CKH中,则有x2=(4-x)2+32,
解得x=![]() ,
,
∴AK=CK=![]() ,
,
∵∠ADK=∠ADC,∠DAK=∠ACD,
∴△ADK∽△CDA,
∴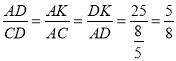 ,设AD=m,DK=n,
,设AD=m,DK=n,
则有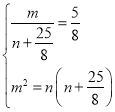 ,解得
,解得![]() .
.
∴AD=![]() .
.
(3)结论:AD:BE=5:6值不变.
理由:∵∠GBE=∠ABC,∠BAC+2∠ABC=180°,∠GBE+∠EBC+∠ABC=180°,
∴∠EBC=∠BAC,
∵∠EDC=∠BAC,
∴∠EBC=∠EDC,
∴D,B,E,C四点共圆,
∴∠EDB=∠ECB,
∵∠EDB+∠EDC=∠ACD+∠DAC,∠EDC=∠DAC,
∴∠EDB=∠ACD,
∴∠ECB=∠ACD,
∴△ACD∽△BCE,
∴![]() .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
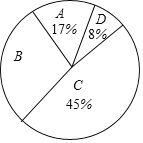
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(单位:千克)与每千克售价x(单位:元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 45 | 50 | 60 |
销售量y(千克) | 110 | 100 | 80 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为w(单位:元),则当每千克售价x定为多少元时,超市每天能获得的利润最大?最大利润是多少元?