题目内容
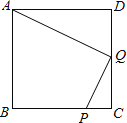
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 上的点,且
上的点,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)![]() 与
与![]() 是否相似?为什么?
是否相似?为什么?
(2)![]() 与
与![]() 的关系是什么?请说明理由.
的关系是什么?请说明理由.
【答案】(1)相似,理由见解析;(2)![]() 且
且![]() ⊥
⊥![]() ,理由见解析
,理由见解析
【解析】
(1)在所要求证的两个三角形中,已知的等量条件为:∠D=∠C=90°,若证明两三角形相似,可证两个三角形的对应直角边成比例;
(2)AQ=2PQ,且AQ⊥PQ.根据相似三角形的对应边成比例即可求得AQ与PQ的数量关系;根据相似三角形的对应角相等即可证得AQ与PQ的位置关系.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠C=∠D=90°;
又∵Q是CD中点,
∴CQ=DQ=![]() AD;
AD;
∵BP=3PC,
∴CP=![]() BC=
BC=![]() AD,
AD,
∴![]() ,
,
又∵∠C=∠D=90°,
∴△ADQ∽△QCP;
(2)AQ=2PQ,且AQ⊥PQ.理由如下:
由(1)知,△ADQ∽△QCP,![]() ,
,
则![]() ,
,
∴AQ=2PQ;
∵△ADQ∽△QCP,
∴∠AQD=∠QPC,∠DAQ=∠PQC,
∴∠PQC+∠DQA=DAQ+AQD=90°,
∴AQ⊥QP.
故![]() 与
与![]() 的关系是:
的关系是:![]() 且
且![]() ⊥
⊥![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(单位:千克)与每千克售价x(单位:元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 45 | 50 | 60 |
销售量y(千克) | 110 | 100 | 80 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为w(单位:元),则当每千克售价x定为多少元时,超市每天能获得的利润最大?最大利润是多少元?
【题目】阅读材料:
工厂加工某种新型材料,首先要将材料进行加温处理,使这种材料保持在一定的温度范围内方可进行继续加工![]() 处理这种材料时,材料温度
处理这种材料时,材料温度![]() 是时间
是时间![]() 的函数
的函数![]() 下面是小明同学研究该函数的过程,把它补充完整:
下面是小明同学研究该函数的过程,把它补充完整:
![]() 在这个函数关系中,自变量x的取值范围是______.
在这个函数关系中,自变量x的取值范围是______.
![]() 如表记录了17min内10个时间点材料温度y随时间x变化的情况:
如表记录了17min内10个时间点材料温度y随时间x变化的情况:
时间 | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
|
温度 | 15 | 24 | 42 | 60 |
|
|
|
| m |
|
|
上表中m的值为______.
![]() 如图,在平面直角坐标系xOy中,已经描出了上表中的部分点
如图,在平面直角坐标系xOy中,已经描出了上表中的部分点![]() 根据描出的点,画出该函数的图象.
根据描出的点,画出该函数的图象.
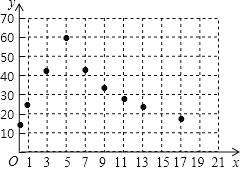
![]() 根据列出的表格和所画的函数图象,可以得到,当
根据列出的表格和所画的函数图象,可以得到,当![]() 时,y与x之间的函数表达式为______,当
时,y与x之间的函数表达式为______,当![]() 时,y与x之间的函数表达式为______.
时,y与x之间的函数表达式为______.
![]() 根据工艺的要求,当材料的温度不低于
根据工艺的要求,当材料的温度不低于![]() 时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.
时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.