题目内容
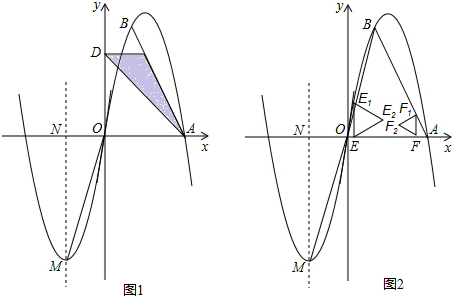
如图,已知抛物线C经过原点,对称轴x=-3与抛物线相交于第三象限的点M,与x轴相交于点N,且tan∠MON=3.
(1)求抛物线C的解析式;
(2)将抛物线C绕原点O旋转180°得到抛物线C′,抛物线C′与x轴的另一交点为A,B为抛物线C′上横坐标为2的点.
①若P为线段AB上一动点,PD⊥y轴于点D,求△APD面积的最大值;
②过线段OA上的两点E,F分别作x轴的垂线,交折线O-B-A于点E1,F1,再分别以线段EE1,FF1为边作如图2所示的等边△EE1E2,等边△FF1F2.点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动.当△EE1E2与△FF1F2的某一边在同一直线上时,求时间t的值.
(1)求抛物线C的解析式;
(2)将抛物线C绕原点O旋转180°得到抛物线C′,抛物线C′与x轴的另一交点为A,B为抛物线C′上横坐标为2的点.
①若P为线段AB上一动点,PD⊥y轴于点D,求△APD面积的最大值;
②过线段OA上的两点E,F分别作x轴的垂线,交折线O-B-A于点E1,F1,再分别以线段EE1,FF1为边作如图2所示的等边△EE1E2,等边△FF1F2.点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动.当△EE1E2与△FF1F2的某一边在同一直线上时,求时间t的值.

(1)∵对称轴MN的解析式为x=-3,∴ON=3,
∵tan∠MON=3,∴MN=9,
∴M(-3,-9),
∴设抛物线C的解析式为y=a(x+3)2-9,
∵抛物线C经过原点,∴0=a(0+3)2-9,解得a=1,
∴抛物线C的解析式为y=(x+3)2-9,即y=x2+6x;
(2)①∵将抛物线C绕原点O旋转180°得到抛物线C′,
∴抛物线C与抛物线C′关于原点O对称,
∴抛物线C′的解析式为y=-x2+6x,
∵当y=0时,x=0或6,
∴点A的坐标为(6,0),
∵点B在抛物线C′上,且其横坐标为2,
∴y=-22+6×2=8,即点B的坐标为(2,8).
设直线AB的解析式为y=kx+b,
则
,
解得
.
∴直线AB的解析式为y=-2x+12,
∵点P在线段AB上,
∴设点P的坐标为(p,-2p+12),
∴S△APD=
p(-2p+12)=-p2+6p=-(p-3)2+9,
∴当p=3时,△APD面积的最大值为9;
②如图,分别过点E2、F2作x轴的垂线,垂足分别为G、H.
根据(2)①知,直线OB解析式为y=4x,直线AB解析式为y=-2x+12.
当0<t≤2时,E1在OB上,F1在AB上,
OE=t,EE1=4t,EG=2
t,OG=t+2
t,GE2=2t,
OF=6-t,FF1=2t,HF=
t,OH=6-t-
t,HF2=t,
∴E(t,0),E1(t,4t),E2(t+2
t,2t),
F(6-t,0),F1(6-t,2t),F2(6-t-
t,t).
(Ⅰ)若EE1与FF1在同一直线上,由t=6-t,得t=3,不符合0<t≤2;
(Ⅱ)若EE2与F1F2在同一直线上,易求得直线EE2的解析式为y=
x-
t,
将F1(6-t,2t)代入,得2t=
×(6-t)-
t,
解得t=
;
(Ⅲ)若E1E2与FF2在同一直线上,易求得E1E2的解析式为y=-
x+4t+
t,
将F(6-t,0)代入,得0=-
×(6-t)+4t+
t,
解得t=
;
当2<t≤4时,E1,F1都在AB上,
OE=t,EE1=12-2t,EG=6
-
t,OG=6
-
t+t,GE2=6-t,
OF=6-t,FF1=2t,HF=
t,OH=6-t-
t,HF2=t,
∴E(t,0),E1(t,12-2t),E2(6
-
t+t,6-t),
F(6-t,0),F1(6-t,2t),F2(6-t-
t,t).
(Ⅰ)若EE1与FF1在同一直线上,由t=6-t,得t=3;
(Ⅱ)若EE2与F1F2在同一直线上,易求得直线EE2的解析式为y=
x-
t,
将F1(6-t,2t)代入,得2t=
×(6-t)-
t,
解得t=
,不符合2<t≤4;
(Ⅲ)E1E2与FF2已知在0<t≤2时同一直线上,故当2<t≤4时,E1E2与FF2不可能在同一直线上;
当4<t<6时,由上面讨论的结果,△EE1E2与△FF1F2的某一边不可能在同一直线上.
综上所述,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,t的值为
或
或3.

∵tan∠MON=3,∴MN=9,
∴M(-3,-9),
∴设抛物线C的解析式为y=a(x+3)2-9,
∵抛物线C经过原点,∴0=a(0+3)2-9,解得a=1,
∴抛物线C的解析式为y=(x+3)2-9,即y=x2+6x;
(2)①∵将抛物线C绕原点O旋转180°得到抛物线C′,
∴抛物线C与抛物线C′关于原点O对称,
∴抛物线C′的解析式为y=-x2+6x,
∵当y=0时,x=0或6,
∴点A的坐标为(6,0),
∵点B在抛物线C′上,且其横坐标为2,
∴y=-22+6×2=8,即点B的坐标为(2,8).
设直线AB的解析式为y=kx+b,
则
|
解得
|
∴直线AB的解析式为y=-2x+12,
∵点P在线段AB上,
∴设点P的坐标为(p,-2p+12),
∴S△APD=
| 1 |
| 2 |
∴当p=3时,△APD面积的最大值为9;
②如图,分别过点E2、F2作x轴的垂线,垂足分别为G、H.
根据(2)①知,直线OB解析式为y=4x,直线AB解析式为y=-2x+12.
当0<t≤2时,E1在OB上,F1在AB上,
OE=t,EE1=4t,EG=2
| 3 |
| 3 |
OF=6-t,FF1=2t,HF=
| 3 |
| 3 |
∴E(t,0),E1(t,4t),E2(t+2
| 3 |
F(6-t,0),F1(6-t,2t),F2(6-t-
| 3 |
(Ⅰ)若EE1与FF1在同一直线上,由t=6-t,得t=3,不符合0<t≤2;
(Ⅱ)若EE2与F1F2在同一直线上,易求得直线EE2的解析式为y=
| ||
| 3 |
| ||
| 3 |
将F1(6-t,2t)代入,得2t=
| ||
| 3 |
| ||
| 3 |
解得t=
3(
| ||
| 2 |
(Ⅲ)若E1E2与FF2在同一直线上,易求得E1E2的解析式为y=-
| ||
| 3 |
| ||
| 3 |
将F(6-t,0)代入,得0=-
| ||
| 3 |
| ||
| 3 |
解得t=
6
| ||
| 11 |
当2<t≤4时,E1,F1都在AB上,
OE=t,EE1=12-2t,EG=6
| 3 |
| 3 |
| 3 |
| 3 |
OF=6-t,FF1=2t,HF=
| 3 |
| 3 |
∴E(t,0),E1(t,12-2t),E2(6
| 3 |
| 3 |
F(6-t,0),F1(6-t,2t),F2(6-t-
| 3 |
(Ⅰ)若EE1与FF1在同一直线上,由t=6-t,得t=3;
(Ⅱ)若EE2与F1F2在同一直线上,易求得直线EE2的解析式为y=
| ||
| 3 |
| ||
| 3 |
将F1(6-t,2t)代入,得2t=
| ||
| 3 |
| ||
| 3 |
解得t=
3(
| ||
| 2 |
(Ⅲ)E1E2与FF2已知在0<t≤2时同一直线上,故当2<t≤4时,E1E2与FF2不可能在同一直线上;
当4<t<6时,由上面讨论的结果,△EE1E2与△FF1F2的某一边不可能在同一直线上.
综上所述,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,t的值为
3(
| ||
| 2 |
6
| ||
| 11 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

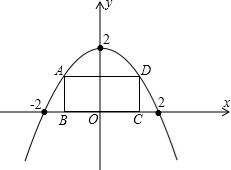 x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.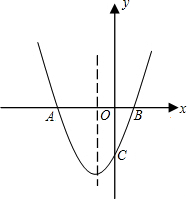
 抛物线对称轴为直线x=-3.
抛物线对称轴为直线x=-3.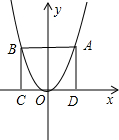 点的坐标(用含有a、b、c的代数式表示)
点的坐标(用含有a、b、c的代数式表示) 的厚度)
的厚度) ,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形ABCD的羊圈.
,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形ABCD的羊圈.