题目内容
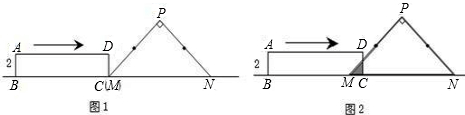
某养殖专业户计划利用房屋的一面墙修造如图所示的长方体水池,培育不同品种的鱼苗.他已准备可以修高为3m.长30m的水池墙的材料,图中EF与房屋的墙壁互相垂直,设AD的长为xm.(不考虑水池墙 的厚度)
的厚度)
(1)请直接写出AB的长(用含有x的代数式表示);
(2)试求水池的总容积V与x的函数关系式,并写出x的取值范围;
(3)如果房屋的墙壁可利用的长度为10.5m,请利用函数图象与性质求V的最大值.
 的厚度)
的厚度)(1)请直接写出AB的长(用含有x的代数式表示);
(2)试求水池的总容积V与x的函数关系式,并写出x的取值范围;
(3)如果房屋的墙壁可利用的长度为10.5m,请利用函数图象与性质求V的最大值.
(1)由题意得:AB=30-3x(3分)
(2)由(1)知V与x的函数关系式为:V=3×x(30-3x)(5分)=-9x2+90x(6分)30-3x>0,x<10(7分)
∴x的取值范围是:0<x<10(8分)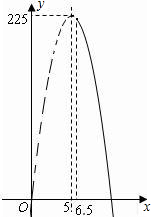
(3)30-3x≤10.5,解得x≥6.5(9分)
V=-9x2+90x=-9(x-5)2+225(10分)
∵a=-9<0
∴函数图象是第一象限内开口向下的抛物线,对称轴为x=5,
当x≥5时,V随x的增大而减小(11分)
又∵6.5>5,由左图可知,
∴当x=6.5时,V取得最大值,(12分)
此时V最大值=-9(x-5)2+225=-9(6.5-5)2+225=204.75.(13分)
(2)由(1)知V与x的函数关系式为:V=3×x(30-3x)(5分)=-9x2+90x(6分)30-3x>0,x<10(7分)
∴x的取值范围是:0<x<10(8分)

(3)30-3x≤10.5,解得x≥6.5(9分)
V=-9x2+90x=-9(x-5)2+225(10分)
∵a=-9<0
∴函数图象是第一象限内开口向下的抛物线,对称轴为x=5,
当x≥5时,V随x的增大而减小(11分)
又∵6.5>5,由左图可知,
∴当x=6.5时,V取得最大值,(12分)
此时V最大值=-9(x-5)2+225=-9(6.5-5)2+225=204.75.(13分)

练习册系列答案
相关题目
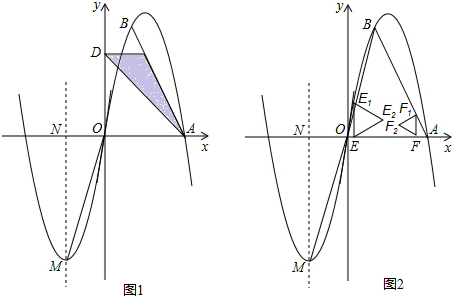

 (x1<0<x2),与y轴交于C点
(x1<0<x2),与y轴交于C点