��Ŀ����
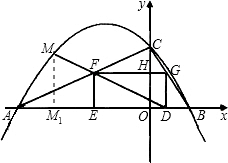
��ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��B����y�ύ�ڵ�C��OC=4��AO=2OC���� �����߶Գ���Ϊֱ��x=-3��
�����߶Գ���Ϊֱ��x=-3��
��1����������ߵĺ�������ʽ��
��2����֪����DEFG��һ����DE���߶�AB�ϣ�����F��G�ֱ���AC��BC�ϣ���OD=m������DEFG�����ΪS��������DEFG�����Sȡ���ֵʱ������DF���ӳ�����M��ʹFM=
DF�������ʱ��M�����ꣻ
��3������Q����������һ�㣬�Һ�����Ϊ-4����P��y����һ�㣬�Ƿ���������ĵ�P��ʹ�á�BPQ��ֱ�������Σ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
 �����߶Գ���Ϊֱ��x=-3��
�����߶Գ���Ϊֱ��x=-3����1����������ߵĺ�������ʽ��
��2����֪����DEFG��һ����DE���߶�AB�ϣ�����F��G�ֱ���AC��BC�ϣ���OD=m������DEFG�����ΪS��������DEFG�����Sȡ���ֵʱ������DF���ӳ�����M��ʹFM=
| 2 |
| 5 |
��3������Q����������һ�㣬�Һ�����Ϊ-4����P��y����һ�㣬�Ƿ���������ĵ�P��ʹ�á�BPQ��ֱ�������Σ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��1����OC=4��
���C��������0��4����
��c=4���������߽���ʽΪy=ax2+bx+4��
��AO=2OC����AO=8��
���A��������-8��0����
�֡������߶Գ���Ϊֱ��x=-3��
���B��������2��O����
��
��
���
��
��������ߵĺ�������ʽΪy=-
x2-
x+4����3�֣�
��2���߾���DEFG��FG��ED����FG��y�ύ�ڵ�H��
���CFH����CAO����CHG����COB��
��
=
=
����
=
��
��FH=4m����FG=5m��
��ֱ��BC�Ľ���ʽΪ��y=kx+b1����
��
���
��
��ֱ��BC�Ľ���ʽΪy=-2x+4�����G������Ϊ��m��-2m+4��
��S=FG��GD=5m��-2m+4��=-10��m-1��2+10��5�֣�
��0��m��2��
�൱m=1ʱ��S���ʱOD=1��OE=4����DE=5��
��M��MM1��x����M1�����MM1D����FED��
��
=
=
��FM=
DF��
��
=
����
=
=
��
��MM1=
��DM1=7����OM1=6��
���ʱ��M������Ϊ(-6��
)����7�֣�
��3�����ڣ��������£�
�ߵ�Q���������ϣ��Һ�����Ϊ-4��
��yQ=6��
���Q������-4��6����
��P������Ϊ��0��n�����ڡ�BPQ�У�
����BQPΪֱ�ǣ���PQ2+BQ2=BP2��
��42+��n-6��2+62+��2+4��2=22+n2��
���n=10��
��ʱ��P������Ϊ��0��10������8�֣�
����QBPΪֱ�ǣ���PQ2=BQ2+BP2��
��42+��6-n��2=62+��2+4��2+22+n2��
���n=-2��
��ʱ��P������Ϊ��0��-2������9�֣�
����QPBΪֱ�ǣ���BQ2=BP2+PQ2��
��62+��2+4��2=42+��n-6��2+22+n2��
���n1=3+
��n2=3-
��ʱ��P������Ϊ(0��3+
)��(0��3-
)����11�֣�
�������������������ĵ�P��ʹ���ԡ�BPQ��ֱ�������Σ�����ĵ�P������Ϊ��
��O��10����0��-2����(0��3+
)��(0��3-
)��
���C��������0��4����
��c=4���������߽���ʽΪy=ax2+bx+4��
��AO=2OC����AO=8��
���A��������-8��0����
�֡������߶Գ���Ϊֱ��x=-3��
���B��������2��O����
��
|
���
|
��������ߵĺ�������ʽΪy=-
| 1 |
| 4 |
| 3 |
| 2 |
��2���߾���DEFG��FG��ED����FG��y�ύ�ڵ�H��
���CFH����CAO����CHG����COB��
��
| FH |
| AO |
| CH |
| CO |
| HG |
| OB |
| FH |
| 8 |
| m |
| 2 |
��FH=4m����FG=5m��
��ֱ��BC�Ľ���ʽΪ��y=kx+b1����
|
���
|
��ֱ��BC�Ľ���ʽΪy=-2x+4�����G������Ϊ��m��-2m+4��
��S=FG��GD=5m��-2m+4��=-10��m-1��2+10��5�֣�
��0��m��2��
�൱m=1ʱ��S���ʱOD=1��OE=4����DE=5��
��M��MM1��x����M1�����MM1D����FED��
��
| MM1 |
| FE |
| MD |
| DF |
| DM1 |
| DE |
��FM=
| 2 |
| 5 |
��
| MD |
| DF |
| 7 |
| 5 |
| MM1 |
| 2 |
| DM1 |
| 5 |
| 7 |
| 5 |
��MM1=
| 14 |
| 5 |
���ʱ��M������Ϊ(-6��
| 14 |
| 5 |
��3�����ڣ��������£�
�ߵ�Q���������ϣ��Һ�����Ϊ-4��
��yQ=6��
���Q������-4��6����
��P������Ϊ��0��n�����ڡ�BPQ�У�
����BQPΪֱ�ǣ���PQ2+BQ2=BP2��
��42+��n-6��2+62+��2+4��2=22+n2��
���n=10��
��ʱ��P������Ϊ��0��10������8�֣�
����QBPΪֱ�ǣ���PQ2=BQ2+BP2��
��42+��6-n��2=62+��2+4��2+22+n2��
���n=-2��
��ʱ��P������Ϊ��0��-2������9�֣�
����QPBΪֱ�ǣ���BQ2=BP2+PQ2��
��62+��2+4��2=42+��n-6��2+22+n2��
���n1=3+
| 17 |
| 17 |
��ʱ��P������Ϊ(0��3+
| 17 |
| 17 |
�������������������ĵ�P��ʹ���ԡ�BPQ��ֱ�������Σ�����ĵ�P������Ϊ��
��O��10����0��-2����(0��3+
| 17 |
| 17 |


��ϰ��ϵ�д�
 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
�����Ŀ


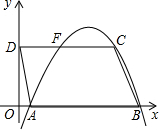 ��F���߶�AD����ֱ�ߵĺ�������ʽΪy=-3x+3��
��F���߶�AD����ֱ�ߵĺ�������ʽΪy=-3x+3�� ��l�ڵ�P��MΪ�������ߵĶ��㣮���ı���PEMF����һ���ڽ�Ϊ60������Σ���������ߵĽ���ʽ��
��l�ڵ�P��MΪ�������ߵĶ��㣮���ı���PEMF����һ���ڽ�Ϊ60������Σ���������ߵĽ���ʽ��
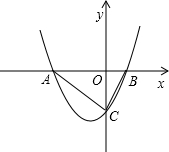 ��x1��0��x2������y�ύ��C��
��x1��0��x2������y�ύ��C��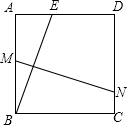 M����DC��N��
M����DC��N��