题目内容
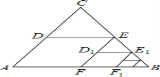
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2017=____.
【答案】![]() .
.
【解析】
根据已知条件利用相似三角形的性质和三角形的面积公式,可求出S1=1,同理可求出S2=![]() ,S3=
,S3=![]() ,每一个四边形的面积都是上一个四边形面积的
,每一个四边形的面积都是上一个四边形面积的![]() ,根据此规律即可求出S2017.
,根据此规律即可求出S2017.
解:∵∠C=90°,AC=BC=2,
∴△ABC的面积为:![]() ×2×2=2,
×2×2=2,
∵点E为BC边中点,ED∥AB,
∴△CDE∽△CAB,
∴![]() ,
,
∴S△CDE=![]() ,
,
又∵EF∥AC,点E为BC边中点,
∴S△BEF=![]() ,
,
∴S1=1,
同理,S2=![]() ,S3=
,S3=![]() ,每一个四边形的面积都是上一个四边形面积的
,每一个四边形的面积都是上一个四边形面积的![]() ,
,
以此类推,S2017=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目