��Ŀ����
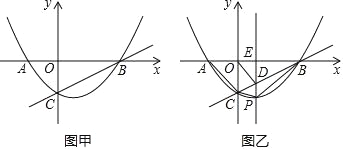
����Ŀ����ͼ�ף�������y��ax2+bx��1����A(��1��0)��B(2��0)���㣬��y���ڵ�C��
(1)�������ߵı���ʽ��ֱ��BC�ı���ʽ��
(2)��ͼ�ң���PΪ�ڵ����������������ϵ�һ�����㣬����P��x��Ĵ���PE��ֱ��BC�ڵ�D��
���ڵ�P�˶������У��ı���ACPB������Ƿ�������ֵ�������ڣ����������ֵ���������ڣ�˵�����ɣ�
���Ƿ���ڵ�Pʹ���Ե�O��C��DΪ������������ǵ��������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
���𰸡�(1)y��![]() x2��
x2��![]() x��1��y��
x��1��y��![]() x��1��(2)�ٵ�x��1ʱ��S���ֵΪ2���ڵ�P����Ϊ(
x��1��(2)�ٵ�x��1ʱ��S���ֵΪ2���ڵ�P����Ϊ(![]() ��
��![]() )��(1����1)��(
)��(1����1)��(![]() ����
����![]() )��
)��
��������
(1)�裺���κ����ı���ʽΪ��y��a(x+1)(x��2)��ax2��ax��2a��������2a����1����ã�a��![]() ��������⣻
��������⣻
(2)��S�ı���ACPB��S��ABC+S��BCP��![]() ��AB��OC+
��AB��OC+![]() ��PD��OB��������⣻�ڷ�CD��OC��CD��OD��OC��OD��������ֱ���⼴�ɣ�
��PD��OB��������⣻�ڷ�CD��OC��CD��OD��OC��OD��������ֱ���⼴�ɣ�
�⣺(1)���κ����ı���ʽΪ��y��a(x+1)(x��2)��ax2��ax��2a��
������2a����1����ã�a��![]() ��
��
�������ߵı���ʽΪ��y��![]() x2��
x2��![]() x��1����C(0����1)��
x��1����C(0����1)��
��ֱ��BC�ı���ʽΪ��y��kx��1��
����B�����������ʽ�ã�0��2k��1����ã�k��![]() ��
��
��ֱ��BC�ı���ʽΪ��y��![]() x��1��
x��1��
(2)�����P(x��![]() x2��
x2��![]() x��1)�����D(x��
x��1)�����D(x��![]() x��1)��
x��1)��
S�ı���ACPB��S��ABC+S��BCP��![]() ��AB��OC+
��AB��OC+![]() ��PD��OB
��PD��OB
��![]() ��3��1+
��3��1+![]() ��2(
��2(![]() x��1��
x��1��![]() x2+
x2+![]() x+1)����
x+1)����![]() x2+x+
x2+x+![]() ��
��
�ߩ�![]() <0��
<0��
��S�����ֵ����x��1ʱ��S���ֵΪ2��
�����D����Ϊ(m��![]() m��1)��
m��1)��
��CD2��m2+![]() m2��OC2��1��DO2��m2+(
m2��OC2��1��DO2��m2+(![]() m��1)2��
m��1)2��![]() m2��m+1��
m2��m+1��
��CD��OCʱ��m2+![]() m2��1����ã�m��
m2��1����ã�m��![]() ��
��
ͬ���ɵã�
��CD��ODʱ��m��1��
��OC��ODʱ��m��![]() ��
��
���P����Ϊ(![]() ��
��![]() )��(1����1)��(
)��(1����1)��(![]() ����
����![]() )��
)��

 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�