题目内容
【题目】正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,

(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
【答案】(1)证明见解析;(2)当![]() 时,四边形
时,四边形![]() 面积最大为10;(3)当点
面积最大为10;(3)当点![]() 运动到
运动到![]() 的中点时,
的中点时,![]() ,此时
,此时![]() .
.
【解析】
试题(1)、根据AM⊥MN得出∠CMN+∠AMB= 90°,根据Rt△ABM得出∠CMN=∠MAB,从而得出三角形相似;(2)、根据三角形相似得出CN与x的关系,然后根据梯形的面积计算法则得出函数解析式;(3)、根据要使三角形相似则需要满足![]() ,结合(1)中的条件得出BM=CM,即M为BC的中点.
,结合(1)中的条件得出BM=CM,即M为BC的中点.
试题解析:(1)在正方形ABCD中,AB=BC=CD=4,∠B=∠C =90°,
∵AM⊥MN ∴∠AMN= 90°. ∴∠CMN+∠AMB= 90°.
在Rt△ABM中,∠MAB+∠AMB=90°, ∴∠CMN=∠MAB. ∴Rt△AMN∽Rt△MCN;
(2)∵Rt△ABM∽Rt△MCN, ∴![]() ∴
∴![]() ∴CN=
∴CN=![]()
∴y=![]() =
=![]() =
=![]()
当x=2时,y取最大值,最大值为10;故当点肘运动到BC的中点时,四边形ABCN的面积最大,最大面积为10;
(3)∵∠B=∠AMN= 90°, ∴要使Rt△ABM∽Rt△AMN,必须 有![]()
由(1)知![]() ∴BM=MC
∴BM=MC
∴当点M运动到BC的中点时,Rt△ABM∽Rt△AMN,此时x=2

【题目】某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人数) |
A | 80≤x<100 | 6 |
B | 100≤x<120 | 8 |
C | 120≤x<140 | m |
D | 140≤x<160 | 18 |
E | 160≤x<180 | 6 |
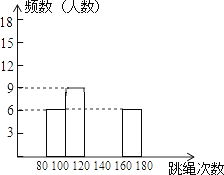
请结合图表解答下列问题:
(1)表中的m=________;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.