Question

【题目】在平面直角坐标系中，抛物线y＝﹣6x+4的顶点A在直线y＝kx﹣2上．

（1）求直线的函数表达式；

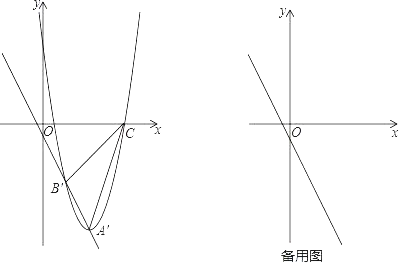
（2）现将抛物线沿该直线方向进行平移，平移后的抛物线的顶点为A′，与直线的另一交点为B′，与x轴的右交点为C（点C不与点A′重合），连接B′C、A′C．

ⅰ）如图，在平移过程中，当点B′在第四象限且△A′B′C的面积为60时，求平移的距离AA′的长；

ⅱ）在平移过程中，当△A′B′C是以A′B′为一条直角边的直角三角形时，求出所有满足条件的点A′的坐标．

Answer 1

【答案】（1）y＝﹣2x﹣2；（2）ⅰ）2；ⅱ）点A′的坐标为（，﹣）或（﹣，﹣）

【解析】

（1）利用配方法将抛物线表达式变形为顶点式，由此可得出点A的坐标，根据点A的坐标，利用待定系数法即可求出直线的函数表达式；

（2）设点A'的坐标为（m，﹣2m﹣2），则平移后抛物线的函数表达式为y（x﹣m）2﹣2m﹣2，利用一次函数图象上点的坐标特征结合点C在x轴上且点C不与点A'重合，可得出m＞﹣1．

i）联立直线和抛物线的表达式成方程组，通过解方程组可求出点B'的坐标，利用二次函数图象上点的坐标特征可求出点C的坐标，过点C作CD∥y轴，交直线A'B'于点D，由点C的坐标可得出点D的坐标，利用S△A'B'C=S△B'CD﹣S△A'CD=60，即可得出关于t的方程，利用换元法解方程组即可得出m的值，进而可得出点A'的坐标，再由点A的坐标利用两点间的距离公式即可求出结论；

ii）根据点A'、B'、C的坐标，可得出A'B'、A'C、B'C的长度，分∠A'B'C=90°及∠B'A'C=90°两种情况，利用勾股定理可得出关于m的方程，利用换元法解方程即可求出m的值，进而可得出点A'的坐标，此题得解．

（1）∵y6x+4（x﹣6）2﹣14，∴点A的坐标为（6，﹣14）．

∵点A在直线y=kx﹣2上，∴﹣14=6k﹣2，解得：k=﹣2，∴直线的函数表达式为y=﹣2x﹣2．

（2）设点A'的坐标为（m，﹣2m﹣2），则平移后抛物线的函数表达式为y（x﹣m）2﹣2m﹣2．

当y=0时，有﹣2x﹣2=0，解得：x=﹣1．

∵平移后的抛物线与x轴的右交点为C（点C不与点A'重合），∴m＞﹣1．

i）联立直线与抛物线的表达式成方程组，，解得：，∴点B'的坐标为（m﹣4，﹣2m+6）．

当y=0时，有（x﹣m）2﹣2m﹣2=0，解得：x1=m﹣2，x2=m+2，∴点C的坐标为（m+2，0）．

过点C作CD∥y轴，交直线A'B'于点D，如图所示．

当x=m+2时，y=﹣2x﹣2=﹣2m﹣42，∴点D的坐标为（m+2，﹣2m﹣42），∴CD=2m+2+4，∴S△A'B'C=S△B'CD﹣S△A'CDCD[m+2（m﹣4）]CD（m+2m）=2CD=2（2m+2+4）=60．

设t，则有t2+2t﹣15=0，解得：t1=﹣5（舍去），t2=3，∴m=8，∴点A'的坐标为（8，﹣18），∴AA'．

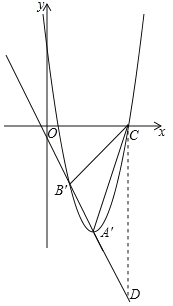
ii）∵A'（m，﹣2m﹣2），B'（m﹣4，﹣2m+6），C（m+2，0），∴A'B'2=（m﹣4﹣m）2+[﹣2m+6﹣（﹣2m﹣2）]2=80，A'C2=（m+2m）2+[0﹣（﹣2m﹣2）]2=4m2+12m+8，B'C2=[m+2（m﹣4）]2+[0﹣（﹣2m+6）]2=4m2﹣20m+56+16．

当∠A'B'C=90°时，有A'C2=A'B'2+B'C2，即4m2+12m+8=80+4m2﹣20m+56+16，整理得：32m﹣128﹣160．

设a，则有2a2﹣a﹣10=0，解得：a1=﹣2（舍去），a2，∴m，∴点A'的坐标为（）；

当∠B'A'C=90°时，有B'C2=A'B'2+A'C2，即4m2﹣20m+56+1680+4m2+12m+8，整理得：32m+32﹣160．

设a，则有2a2﹣a=0，解得：a3=0（舍去），a4，∴m，∴点A'的坐标为（）．

综上所述：在平移过程中，当△A'B'C是以A'B'为一条直角边的直角三角形时，点A'的坐标为（）或（）．