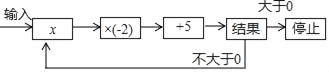
题目内容
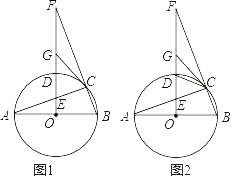
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. 2B. 8C. ![]() D. 2
D. 2![]()
【答案】D
【解析】
连结BE,设⊙O的半径为R,由OD⊥AB,根据垂径定理得AC=BC=![]() AB=4,在Rt△AOC中,OA=R,OC=R﹣CD=R﹣2,根据勾股定理得到(R﹣2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
AB=4,在Rt△AOC中,OA=R,OC=R﹣CD=R﹣2,根据勾股定理得到(R﹣2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
解:连结BE,设⊙O的半径为R,如图,
∵OD⊥AB,
∴AC=BC=![]() AB=
AB=![]() ×8=4,
×8=4,
在Rt△AOC中,OA=R,OC=R﹣CD=R﹣2,
∵OC2+AC2=OA2,
∴(R﹣2)2+42=R2,解得R=5,
∴OC=5﹣2=3,
∴BE=2OC=6,
∵AE为直径,
∴∠ABE=90°,
在Rt△BCE中,CE=![]() .
.
故选:D.

 习题精选系列答案
习题精选系列答案【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
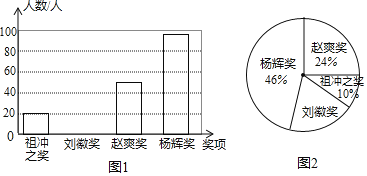
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.