题目内容
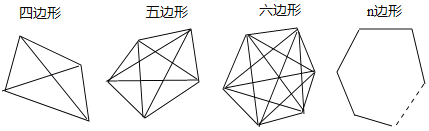
【题目】连接多边形任意两个不相邻顶点的线段称为多边形的对角线．
（1）四、五、六、n边形对角线条数分别为 、 、 、 ．
（2）多边形可以有12条对角线吗？如果可以，求多边形的边数；如果不可以，请说明理由．
（3）若一个n边形的内角和为1800°，求它对角线的条数．
（4）已知k-1边形的对角线条数是
,求k+1边形的对角线条数（k>4）．
【答案】（1）2；5；9；
；（2）没有，见解析；（3）54；（4）
.
【解析】
（1）根据多边形对角线条数公式即可求出结论；
（2）假设可以，根据多边形对角线条数公式，可得出关于n的一元二次方程，解之即可得出结论；
（3）根据多边形内角和定理，可求出边数，再根据多边形对角线条数公式，即可得出结论．
（4）根据n边形对角线的条数公式，把n换成k+1即可．
解：（1）四边形对角线条数为：
五边形对角线条数为：
六边形对角线条数为：
n边形对角线条数为：
故答案为：2；5；9；．
（2）假设有，设多边形的边数为n，则：
∴
-3n-24=0，∴n=
∵n
，且n为整数
∴没有这样的多边形.
（3）∵一个n边形的内角和为1800°，
∴180°×（n﹣2）=1800°，
解得：n=12，
∴
．
答：这个多边形有54条对角线．
（4）∵n边形对角线条数为：
∴k+1边形的对角线条数为：
【题目】小王是“新星厂”的一名工人，请你阅读下列信息：
信息一：工人工作时间：每天上午8：00—12：00，下午14：00—18：00，每月工作25天；
信息二：小王生产甲、乙两种产品的件数与所用时间的关系见下表：
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三：按件计酬，每生产一件甲种产品得1.50元，每生产一件乙种产品得2.80元；
信息四：该厂工人每月收入由底薪和计酬工资两部分构成，小王每月的底薪为1900元．请根据以上信息，解答下列问题：
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟；
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件，则小王该月收入最多是多少元？此时小王生产的甲、乙两种产品分别是多少件？
