题目内容
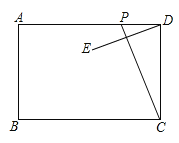
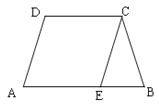
【题目】等腰梯形ABCD中,AB∥DC,AD=BC=CD,点E为AB上一点,连结CE,请添加一个你认为合适的条件 ,使四边形AECD为菱形.
【答案】AE=AD或∠CEB=∠B(答案不唯一).
【解析】
试题已知了四边形ADCE的一组邻边相等,那么ADCE是菱形的前提条件是四边形ADCE为平行四边形,可针对平行四边形的判定方法及等腰梯形的性质来添加所需要的条件.
试题解析:可添加的条件为AE=AD或∠CEB=∠B等(答案不唯一);
以∠CEB=∠B为例进行说明;
证明:∵∠CEB=∠B,
∴BC=CE=AD;
∵四边形ABCD是等腰梯形,
∴∠DAB=∠CEB=∠B;
∴AD平行且相等于CE,即四边形AECD是平行四边形;
又∵AD=DC,
∴平行四边形ADCE是菱形.
考点: 1.菱形的判定;2.等腰梯形的性质.

练习册系列答案
相关题目