��Ŀ����
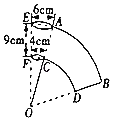
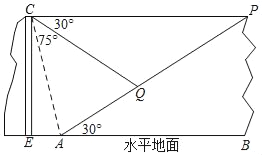
����Ŀ����ͼ��ij���ʹ�������������Сɽ���ο�������Сɽɽ��E��������ֱ�۹��������100����ɽ��C����Ȼ��ȿ�����ˮƽ�۹��Ų��е�����P����Ҳ����ͨ�������������ᄚ��Q������ɽ��C���۲��µ�A�ĸ���Ϊ75�㣬�۲�Q���ĸ���Ϊ30�㣬��֪�Ҳ�Сɽ���½�Ϊ30�㣨ͼ�еĵ�C��E��A��B��P��Q����ͬһƽ���ڣ���A��Q��P��ͬһֱ���ϣ�
��1�����CAP�Ķ�����CP�ij��ȣ�
��2����P��Q����֮��ľ��룮������������ţ�
���𰸡���1��75�㣬200��2��![]()
��������
��1������ƽ���ߵ����ʵõ���APC����PAB��30�������������ε��ڽǺ͵õ���CAP��180�㩁75�㩁30�㣽75�������ݵ��������ε��ж������õ�PC��AP����P��PF��AB��F������ֱ�������ε����ʼ��ɵõ����ۣ���2�����ݵ��������ε��ж������õ�CQ��PQ����Q��QH��PC��H������ֱ�������ε����ʼ��ɵõ����ۣ�
��1����PC��AB��
���APC����PAB��30�㣬
���CAP��180�㩁75�㩁30�㣽75�㣬
���CAP����PCA��
��PC��AP��
��P��PF��AB��F��
��PF��CE��100��
��PA��2PF��200�ף�
��2���ߡ�PCQ����QPC��30�㣬
��CQ��PQ��
��Q��QH��PC��H��
��PH��![]() PC��100��
PC��100��
��PQ��![]() �ף�
�ף�
��P��Q����֮��ľ�����![]() �ף�
�ף�

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�