题目内容
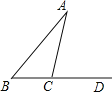
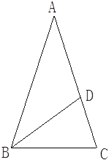
【题目】已知:如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,
(1)求证:△ABC∽△BCD;
(2)若BC=2,求AB的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)根据角平分线的性质得到∠DBC=∠A,已知有一组公共角,则根据有两组角对应相等则两三角形相似可得到△ABC∽△BCD;
(2)相似三角形的对应边对应成比例,且由已知可得到BD=BC=AD,从而便可求得AB的长.
试题解析:(1)∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°.
∴∠DBC=∠A=36°.
又∵∠ABC=∠C,
∴△ABC∽△BCD.
(2)∵∠ABD=∠A=36°,
∴AD=BD,∠BDC=∠C=72°.
∴BD=BC=AD.
∵△ABC∽△BCD,
∴![]() .
.
即![]() .
.
解得:AB=![]() 或
或![]() (不符合题意).
(不符合题意).
∴AB=![]() .
.
考点: 1.等腰三角形的性质;2.角平分线的性质;3.相似三角形的判定与性质.

练习册系列答案
相关题目