题目内容
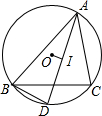
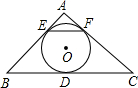
等腰直角三角形ABC中，∠A=90°，⊙O为△ABC的内切圆，D、E、F分别为切点，则
=（ ）
| EF |
| BC |
A．
| B．
| C．
| D．
|
∵⊙O为△ABC的内切圆，
∴AE=AF，BD=BE，CD=CF，
∵等腰直角三角形ABC中，∠A=90°，
∴BD=DC，△AEF为等腰直角三角形，
∴△AEF∽△ABC，
设AB=AC=a，
∴BC=
a，
∴BD=CD=BE=CF=
a，
∴AE=AF=a-
a，
∴EF：BC=AF：AC=（2-
）：2．
故选择C．
∴AE=AF，BD=BE，CD=CF，
∵等腰直角三角形ABC中，∠A=90°，
∴BD=DC，△AEF为等腰直角三角形，
∴△AEF∽△ABC，
设AB=AC=a，
∴BC=
| 2 |
∴BD=CD=BE=CF=
| ||
| 2 |
∴AE=AF=a-
| ||
| 2 |
∴EF：BC=AF：AC=（2-
| 2 |
故选择C．
练习册系列答案
中考解读考点精练系列答案
相关题目
