题目内容

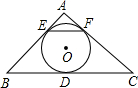
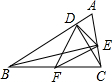
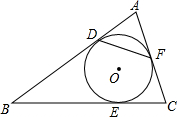
如图，已知△ABC的内切圆O与三边分别切于D、E、F，∠A=60°，CB=6cm，△ABC的周长为16cm，则DF的长等于（　　）
A．2cmB．3cmC．4cmD．6cm

∵△ABC的内切圆O与三边分别切于D、E、F，CB=6cm，△ABC的周长为16cm，
∴BD=BE，CE=CF，AD=AF，
∵BE+EC=BD+FC=6，
∴AD=AF=
1
2
（AB+AC+BC-BC-BD-CF）=
1
2
（16-6-6）=2，
∵∠A=60°，
∴△ADF是等边三角形，
∴DF=2．
故选：A．
练习册系列答案
相关题目
如图所示，某市有一块由三条马路围成的三角形绿地现准备在其中建一小亭供人们休息，要求小亭中心到三条马路的距离相等，试确定小亭的中心位置．（不写作法，保留作图痕迹）
已知AD、BE是△ABC的中线，AD、BE相交于G，若BE=9cm，则BG=______cm．
如图，在边长为2的正三角形中，将其内切圆和三个角切圆（与角两边及三角形内切圆都相切的圆）的内部挖去，则此三角形剩下部分（阴影部分）的面积为______．
某地有四个村庄E，F，G，H（其位置如图所示），现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（圆形区域半径越小，所需功率越小），此中转站应建在（　　）
A．线段HF的中点处B．△GHE的外心处
C．△HEF的外心处D．△GEF的外心处
等腰直角三角形ABC中，∠A=90°，⊙O为△ABC的内切圆，D、E、F分别为切点，则
EF
BC
=（　　）
A．
1
4
B．
1
2
C．
2-
2
2
D．
2-
2
4
解答题：
（1）设互为补角的两个角的差为60°，求较小角的余角．
（2）设一个角的补角是这个角的余角的5倍，求这个角的度数．
（3）如图，∠1=∠2，∠EMB=55°，试求∠DNF的度数．

（4）如图，△ABC三个顶点分别表示三个小区，AB，BC，AC是连接三个小区的已有自来水管道，某工程队现在要△ABC在内部（包括边上）建一个自来水公司M，M到AB，BC，AC的距离和计为L，已知AB=4，BC=5，AC=6，问自来水供应M在哪个位置，工程对才有最大的经济效益（即L最小）
如图，△ABC为锐角三角形，△ABC内接于圆O，∠BAC=60°，H是△ABC的垂心，BD是⊙O的直径．
求证：AH=
1
2
BD．
如图所示，BE，CD是△ABC的两条高，F为BC的中点．那△DEF是（　　）
A．不等边三角形B．等腰三角形
C．等边三角形D．形状不能确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网