Question

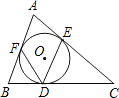
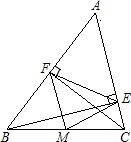
如图，在△ABC中，AD，BE分别是∠A，∠B的角平分线，O是AD与BE的交点，若C，D，O，E四点共圆，DE=3，则△ODE的内切圆半径为______．

Answer 1

作OF⊥ED于点F，
∵AD，BE分别是∠A，∠B的角平分线，
∴∠AOB=90°+

1

2

∠C，CO平分∠ACB，
又∵∠DOE=∠AOB，∠DOE+∠C=180°，
∴∠C=60°，∠DOE=∠AOB=120°，
又∵OD=OE，
∴∠OED=∠ODE=30°，
∴FD=

3

2

，
tan30°=

FO

DF

=

FO

3 2

，
∴FO=

3

2

，OD=OE=

3

，
∴△ODE的周长为：2

3

+3，
∴△ODE的面积为：

1

2

×3×

3

2

=

3 3

4

，
∴△ODE的内切圆半径为

3 3 2

2 3 +3

=3-

3 3

2

．
故答案为：3-

3 3

2

．