题目内容
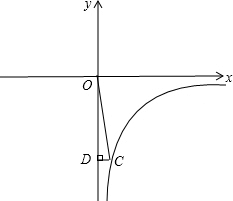
如图,点P是反比例函数y=
(x>0)的图象上的一个动点,PA⊥x轴于点A,延长AP至点B,使PB=PA,过点B作BC⊥y轴于点C,交反比例函数图象于点D.
(1)填空:S△AOP______S△COD(填“>“<”或“=”)
(2)当点P的位置改变时,四边形PODB的面积是否改变?说明理由.
(3)连接OB,交反比例函数y=
(x>0)的图象于点E,试求
的值.

| 2 |
| x |
(1)填空:S△AOP______S△COD(填“>“<”或“=”)
(2)当点P的位置改变时,四边形PODB的面积是否改变?说明理由.
(3)连接OB,交反比例函数y=
| 2 |
| x |
| OE |
| OB |

(1)依题意设P(m,
),则B(m,
),D(
,
),
故S△AOP=
m×
=1,S△COD=
×
×
=1,
即S△AOP=S△COD,
故答案为:=;
(2)不改变.
理由:∵S四边形PODB=S矩形OABC-S△AOP-S△COD=m×
-1-1=2,
∴当点P的位置改变时,四边形PODB的面积总是2,不改变;
(3)设直线OB解析式为y=kx,将B(m,
)代入,得k=
,
可知直线OB解析式为y=
x,
联立
,得
,即E(
,
),
故
=
=
.
| 2 |
| m |
| 4 |
| m |
| m |
| 2 |
| 4 |
| m |
故S△AOP=
| 1 |
| 2 |
| 2 |
| m |
| 1 |
| 2 |
| m |
| 2 |
| 4 |
| m |
即S△AOP=S△COD,
故答案为:=;
(2)不改变.
理由:∵S四边形PODB=S矩形OABC-S△AOP-S△COD=m×
| 4 |
| m |
∴当点P的位置改变时,四边形PODB的面积总是2,不改变;
(3)设直线OB解析式为y=kx,将B(m,
| 4 |
| m |
| 4 |
| m2 |
可知直线OB解析式为y=
| 4 |
| m2 |
联立
|
|
| ||
| 2 |
2
| ||
| m |
故
| OE |
| OB |
| ||||
|
| ||
| 2 |

练习册系列答案
相关题目


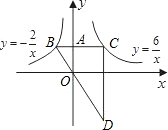 <0)的图象于B,交函数y=
<0)的图象于B,交函数y=