题目内容
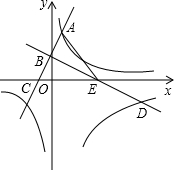
如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=
的图象的一个交点为A(1,m).过点B作AB的垂线BD,与反比例函数y=
(x>0)的图象交于点D(n,-2).
(1)求k1和k2的值;
(2)若直线AB、BD分别交x轴于点C、E,试问在y轴上是否存在一个点F,使得△BDF∽△ACE?若存在,求出点F的坐标;若不存在,请说明理由.
| k1 |
| x |
| k2 |
| x |
(1)求k1和k2的值;
(2)若直线AB、BD分别交x轴于点C、E,试问在y轴上是否存在一个点F,使得△BDF∽△ACE?若存在,求出点F的坐标;若不存在,请说明理由.

(1)将A(1,m)代入一次函数y=2x+2中,得:m=2+2=4,即A(1,4),
将A(1,4)代入反比例解析式y=
得:k1=4;
过A作AM⊥y轴,过D作DN⊥y轴,
∴∠AMB=∠DNB=90°,
∴∠BAM+∠ABM=90°,
∵AC⊥BD,即∠ABD=90°,
∴∠ABM+∠DBN=90°,
∴∠BAM=∠DBN,
∴△ABM∽△BDN,
∴
=
,即
=
,
∴DN=8,
∴D(8,-2),
将D坐标代入y=
得:k2=-16;
(2)符合条件的F坐标为(0,-8),理由为: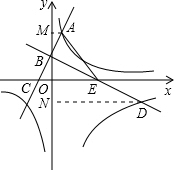
由y=2x+2,求出C坐标为(-1,0),
∵OB=ON=2,DN=8,
∴OE=4,
可得AE=5,CE=5,AC=2
,BD=4
,∠EBO=∠ACE=∠EAC,
若△BDF∽△ACE,则
=
,即
=
,
解得:BF=10,
则F(0,-8).
综上所述:F点坐标为(0,-8)时,△BDF∽△ACE.
将A(1,4)代入反比例解析式y=
| k1 |
| x |
过A作AM⊥y轴,过D作DN⊥y轴,
∴∠AMB=∠DNB=90°,
∴∠BAM+∠ABM=90°,
∵AC⊥BD,即∠ABD=90°,
∴∠ABM+∠DBN=90°,
∴∠BAM=∠DBN,
∴△ABM∽△BDN,
∴
| AM |
| BN |
| BM |
| DN |
| 1 |
| 4 |
| 2 |
| DN |
∴DN=8,
∴D(8,-2),
将D坐标代入y=
| k2 |
| x |
(2)符合条件的F坐标为(0,-8),理由为:

由y=2x+2,求出C坐标为(-1,0),
∵OB=ON=2,DN=8,
∴OE=4,
可得AE=5,CE=5,AC=2
| 5 |
| 5 |
若△BDF∽△ACE,则
| BD |
| AC |
| BF |
| AE |
4
| ||
2
|
| BF |
| 5 |
解得:BF=10,
则F(0,-8).
综上所述:F点坐标为(0,-8)时,△BDF∽△ACE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 3+3
3+3 图象相交于A、B两点.
图象相交于A、B两点.
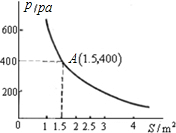 当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
