题目内容
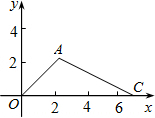
已知,如图点A(1,1),B(2,-3),点P为x轴上一点,当|PA-PB|最大时,点P的坐标为( )

A.(
| B.(
| C.(-
| D.(1,0) |

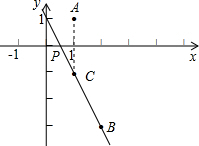
作A关于x轴对称点C,连接BC并延长交x轴于点P,
∵A(1,1),
∴C的坐标为(1,-1),
连接BC,
设直线BC的解析式为:y=kx+b,
∴
,
解得:
,
∴直线BC的解析式为:y=-2x+1,
当y=0时,x=
,
∴点P的坐标为:(
,0),
∵当B,C,P不共线时,根据三角形三边的关系可得:|PA-PB|=|PC-PB|<BC,
∴此时|PA-PB|=|PC-PB|=BC取得最大值.
故选A.
∵A(1,1),
∴C的坐标为(1,-1),
连接BC,
设直线BC的解析式为:y=kx+b,
∴
|
解得:
|
∴直线BC的解析式为:y=-2x+1,
当y=0时,x=
| 1 |
| 2 |
∴点P的坐标为:(
| 1 |
| 2 |
∵当B,C,P不共线时,根据三角形三边的关系可得:|PA-PB|=|PC-PB|<BC,
∴此时|PA-PB|=|PC-PB|=BC取得最大值.
故选A.


练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目

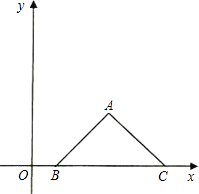 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).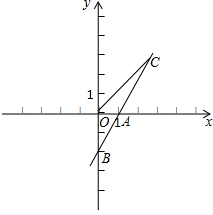

 ,0),以CD为一边在x轴上方作矩形CDEF,且CF:CD=1:2.设矩形CDEF与△ABO重叠部分的面积为S.
,0),以CD为一边在x轴上方作矩形CDEF,且CF:CD=1:2.设矩形CDEF与△ABO重叠部分的面积为S.
 回答下列问题:
回答下列问题: