题目内容
如图,将△ABC放在平面直角坐标系中,使B、C在X轴正半轴上,若AB=AC.且A点坐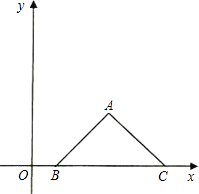 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).
(1)求边AC所在直线的解析式;
(2)若坐标平面内存在三角形与△ABC全等且有一条公共边,请写出这些三角形未知顶点的坐标.
 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).(1)求边AC所在直线的解析式;
(2)若坐标平面内存在三角形与△ABC全等且有一条公共边,请写出这些三角形未知顶点的坐标.
(1)设C点的坐标为(x,0).
∵AB=AC,
∴点A在BC的垂直平分线上,
又∵A点坐标为(3,2),B点坐标为(1,0),
∴
=3,
∴x=5,即C点的坐标为(5,0).
设边AC所在直线的解析式为y=kx+b,则
,
解得
.
故边AC所在直线的解析式y=-x+5;
(2)∵A点坐标为(3,2),B点坐标为(1,0),C点的坐标为(5,0),
∴AB=AC=2
,BC=4,
∴AB2+AC2=BC2,
∴△ABC为等腰直角三角形.
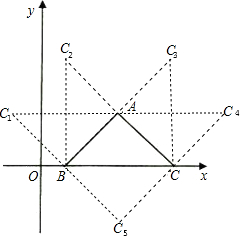
如图所示,符合要求的点有:
C1(-1,2),C2(1,4),C3(5,4),C4(7,2),C5(3,-2).
∵AB=AC,
∴点A在BC的垂直平分线上,
又∵A点坐标为(3,2),B点坐标为(1,0),
∴
| 1+x |
| 2 |
∴x=5,即C点的坐标为(5,0).
设边AC所在直线的解析式为y=kx+b,则
|
解得
|
故边AC所在直线的解析式y=-x+5;
(2)∵A点坐标为(3,2),B点坐标为(1,0),C点的坐标为(5,0),
∴AB=AC=2
| 2 |
∴AB2+AC2=BC2,
∴△ABC为等腰直角三角形.
如图所示,符合要求的点有:
C1(-1,2),C2(1,4),C3(5,4),C4(7,2),C5(3,-2).


练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目


 着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.
着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.