题目内容
如图,在平面直角坐标系中,△ABC为等腰三角形,AB=AC,将△AOC沿直线AC折叠,点O落在直线AD上的点E处,直线AD的解析式为y=-
x+6,则
(1)AO=______;AD=______;OC=______;
(2)动点P以每秒1个单位的速度从点B出发,沿着x轴正方向匀速运动,点Q是射线CE上的点,且∠PAQ=∠BAC,设P运动时间为t秒,求△POQ的面积S与t之间的函数关系式;
(3)在(2)的条件下,直线CE上是否存在一点Q,使以点Q、A、D、P为顶点的四边形是平等四边形?若存在,求出t值及Q点坐标;若不存在,说明理由.

| 3 |
| 4 |
(1)AO=______;AD=______;OC=______;
(2)动点P以每秒1个单位的速度从点B出发,沿着x轴正方向匀速运动,点Q是射线CE上的点,且∠PAQ=∠BAC,设P运动时间为t秒,求△POQ的面积S与t之间的函数关系式;
(3)在(2)的条件下,直线CE上是否存在一点Q,使以点Q、A、D、P为顶点的四边形是平等四边形?若存在,求出t值及Q点坐标;若不存在,说明理由.

(1)∵A、D是直线y=-
x+6上的点,
∴A(0,6),D(8,0),
∴AO=6,OD=8;
∵△AOD是直角三角形,
∴AD=
=
=10,
∵△ACE由△ACO反折而成,
∴AE=AO=6,CE⊥AD,
∴DE=QD-AE=10-6=4,
∵∠ADO=∠ADO,∠AOD=∠CED,
∴△AOD∽△CED,
∴
=
,
=
,解得CD=5,
∴OC=OD-CD=8-5=3.
(2)当P在线段BO上时,即0<t<3时;
∵∠BAC=∠PAQ,
∴∠BAP=∠CAQ=∠BAC-∠PAC=∠PAQ-∠PAC;
又∵∠ABP=∠ACQ=∠ACO,且AB=AC,
∴△ABP≌△ACQ,得BP=CQ=t,OP=3-t;
∴△POQ的面积为:S=
OP•CQ•sin∠ECD=
(3-t)×
t,即S=-
t2+
t;
当P在x轴正半轴上时,即t>3时;
同①可得:BP=CQ=t,OP=t-3;
∴S=
OP•CQ•sin∠ECD=
(t-3)×
t,
即S=
t2-
t;
综上可知:S=
;
(3)分两种情况:
①0<t<3时,显然不存在以AD为边的情况,那么只考虑以AD为对角线的情况;
此时P(t-3,0),取易知AD的中点为:(4,3);
∵平行四边形中,以AD、PQ为对角线,
∴AD的中点也是PQ的中点;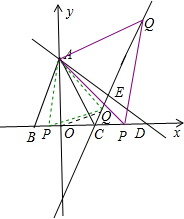
∴Q(11-t,6);
∵直线CE:y=
x-4,代入Q点坐标得:
(11-t)-4=6,解得t=
;即BP=CQ=
,
∴Q(
×
+3,
×
),即Q(
,
);
②t>3时,显然不存在以AD为对角线的情况,那么只考虑以AD为边的情况;
此时PF∥DP,即F点纵坐标为6,由①得,此时F(
,6);
即DP=AF=
,BP=BD+DP=11+
=
,即t=
;
此时CQ=BP=
,同①可求得:Q(
,
).
综上可知:存在符合条件的F点,此时的t值和Q点坐标分别为:t=
,Q(
,
)或t=
,Q(
,
).
故答案为:10,6,3.
| 3 |
| 4 |
∴A(0,6),D(8,0),
∴AO=6,OD=8;
∵△AOD是直角三角形,
∴AD=
| AO2+OD2 |
| 62+82 |
∵△ACE由△ACO反折而成,
∴AE=AO=6,CE⊥AD,
∴DE=QD-AE=10-6=4,
∵∠ADO=∠ADO,∠AOD=∠CED,
∴△AOD∽△CED,
∴
| AD |
| CD |
| OD |
| ED |
| 10 |
| CD |
| 8 |
| 4 |
∴OC=OD-CD=8-5=3.
(2)当P在线段BO上时,即0<t<3时;
∵∠BAC=∠PAQ,

∴∠BAP=∠CAQ=∠BAC-∠PAC=∠PAQ-∠PAC;
又∵∠ABP=∠ACQ=∠ACO,且AB=AC,
∴△ABP≌△ACQ,得BP=CQ=t,OP=3-t;
∴△POQ的面积为:S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 6 |
| 5 |
当P在x轴正半轴上时,即t>3时;
同①可得:BP=CQ=t,OP=t-3;
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
即S=
| 2 |
| 5 |
| 6 |
| 5 |
综上可知:S=
|
(3)分两种情况:
①0<t<3时,显然不存在以AD为边的情况,那么只考虑以AD为对角线的情况;
此时P(t-3,0),取易知AD的中点为:(4,3);
∵平行四边形中,以AD、PQ为对角线,
∴AD的中点也是PQ的中点;

∴Q(11-t,6);
∵直线CE:y=
| 4 |
| 3 |
| 4 |
| 3 |
| 7 |
| 2 |
| 7 |
| 2 |
∴Q(
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
| 4 |
| 5 |
| 51 |
| 10 |
| 14 |
| 5 |
②t>3时,显然不存在以AD为对角线的情况,那么只考虑以AD为边的情况;
此时PF∥DP,即F点纵坐标为6,由①得,此时F(
| 15 |
| 2 |
即DP=AF=
| 15 |
| 2 |
| 15 |
| 2 |
| 37 |
| 2 |
| 37 |
| 2 |
此时CQ=BP=
| 37 |
| 2 |
| 141 |
| 10 |
| 74 |
| 5 |
综上可知:存在符合条件的F点,此时的t值和Q点坐标分别为:t=
| 3 |
| 2 |
| 51 |
| 10 |
| 14 |
| 5 |
| 37 |
| 2 |
| 141 |
| 10 |
| 74 |
| 5 |
故答案为:10,6,3.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目



 而行.设步行时间为x小时,甲、乙两班离A地的距离分别为y1、y2千米,y1、y2与x的函数关系图象如图所示.根据图象解答下列问题:
而行.设步行时间为x小时,甲、乙两班离A地的距离分别为y1、y2千米,y1、y2与x的函数关系图象如图所示.根据图象解答下列问题: