题目内容
【题目】如图，
方格纸中小正方形的边长为1，
，
两点在格点上，要在图中格点上找到点
，使得
的面积为2，满足条件的点有（ ）
A.无数个B.7个C.6个D.5个
【答案】C
【解析】
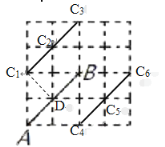
如解图中的C1、D，连接C1D，根据勾股定理即可求出C1D和AB，然后根据三线合一即可求出S△C1AB=2，然后根据平行线之间的距离处处相等即可求出另外两个点C2 、C3，然后同理可找出C4、C5 、C6，从而得出结论．
解：设如下图所示中的两个格点为C1、D，连接C1D
根据勾股定理可得C1D=AD=BD=
，AB=
∵C1A= C1B，点D为AB的中点
∴C1D⊥AB
∴S△C1AB=
AB·C1D=2
∴此时点C1即为所求
过点C1作AB的平行线，交如图所示的格点于C2 、C3，根据平行线之间的距离处处相等，此时C2 、C3也符合题意；
同理可得：S△C4AB=2，
∴点C4即为所求，过点C4作AB的平行线，交如图所示的格点于C5 、C6，根据平行线之间的距离处处相等，此时C4 、C5也符合题意．
满足条件的点C共有6个
故选C．
练习册系列答案
相关题目
