题目内容
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
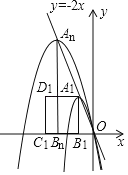
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2,…,Bn,以线段AnBn为边向左作正方形AnBnCnDn,如果这组抛物线中的某一条经过点Dn,求此时满足条件的正方形AnBnCnDn的边长.
【答案】(1)抛物线的表达式为y=﹣3x2﹣6x;(2)b1=﹣4,b2=0;(3)正方形的边长是10.
【解析】试题分析:(1)把点(﹣2,0)和(﹣1,3)分别代入y=ax2+bx,得到关于a、b的二元一次方程组,解方程组即可;
(2)根据二次函数的性质,得出抛物线y=ax2+bx的顶点坐标是(﹣![]() ,﹣
,﹣![]() ),把顶点坐标代入y=﹣2x,得出﹣
),把顶点坐标代入y=﹣2x,得出﹣![]() =﹣2×(﹣
=﹣2×(﹣![]() ),即可求出b的值;
),即可求出b的值;
(3)由于这组抛物线的顶点A1、A2、…,An在直线y=﹣2x上,根据(2)的结论可知,b=4或b=0.①当b=0时,不合题意舍去;②当b=﹣4时,抛物线的表达式为y=ax2﹣4x.由题意可知,第n条抛物线的顶点为An(﹣n,2n),则Dn(﹣3n,2n),因为以An为顶点的抛物线不可能经过点Dn,设第n+k(k为正整数)条抛物线经过点Dn,此时第n+k条抛物线的顶点坐标是An+k(﹣n﹣k,2n+2k),根据﹣![]() =﹣n﹣k,得出a=
=﹣n﹣k,得出a=![]() =﹣
=﹣![]() ,即第n+k条抛物线的表达式为y=﹣
,即第n+k条抛物线的表达式为y=﹣![]() x2﹣4x,根据Dn(﹣3n,2n)在第n+k条抛物线上,得到2n=﹣
x2﹣4x,根据Dn(﹣3n,2n)在第n+k条抛物线上,得到2n=﹣![]() ×(﹣3n)2﹣4×(﹣3n),解得k=
×(﹣3n)2﹣4×(﹣3n),解得k=![]() n,进而求解即可.
n,进而求解即可.
试题解析:(1)∵抛物线y=ax2+bx经过点(﹣2,0)和(﹣1,3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的表达式为y=﹣3x2﹣6x;
(2)∵抛物线y=ax2+bx的顶点坐标是(﹣![]() ,﹣
,﹣![]() ),且该点在直线y=﹣2x上,
),且该点在直线y=﹣2x上,
∴﹣![]() =﹣2×(﹣
=﹣2×(﹣![]() ),
),
∵a≠0,∴﹣b2=4b,
解得b1=﹣4,b2=0;
(3)这组抛物线的顶点A1、A2、…,An在直线y=﹣2x上,
由(2)可知,b=4或b=0.
①当b=0时,抛物线的顶点在坐标原点,不合题意,舍去;
②当b=﹣4时,抛物线的表达式为y=ax2﹣4x.
由题意可知,第n条抛物线的顶点为An(﹣n,2n),则Dn(﹣3n,2n),
∵以An为顶点的抛物线不可能经过点Dn,设第n+k(k为正整数)条抛物线经过点Dn,此时第n+k条抛物线的顶点坐标是An+k(﹣n﹣k,2n+2k),
∴﹣![]() =﹣n﹣k,∴a=
=﹣n﹣k,∴a=![]() =﹣
=﹣![]() ,
,
∴第n+k条抛物线的表达式为y=﹣![]() x2﹣4x,
x2﹣4x,
∵Dn(﹣3n,2n)在第n+k条抛物线上,
∴2n=﹣![]() ×(﹣3n)2﹣4×(﹣3n),解得k=
×(﹣3n)2﹣4×(﹣3n),解得k=![]() n,
n,
∵n,k为正整数,且n≤12,
∴n1=5,n2=10.
当n=5时,k=4,n+k=9;
当n=10时,k=8,n+k=18>12(舍去),
∴D5(﹣15,10),
∴正方形的边长是10.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案